
分析 (1)设与直线3x+4y-7=0垂直的直线方程为:4x-3y+m=0.又与原点的距离为6,可得$\frac{|m|}{\sqrt{{4}^{2}+(-3)^{2}}}$=6,解得m即可.
(2)联立$\left\{\begin{array}{l}{2x+3y-5=0}\\{7x+15y+1=0}\end{array}\right.$,解得交点P的坐标.设平行于直线 x+2y-3=0的直线方程为 x+2y+n=0.代入即可得出.
解答 解:(1)设与直线3x+4y-7=0垂直的直线方程为:4x-3y+m=0.
又与原点的距离为6,
∴$\frac{|m|}{\sqrt{{4}^{2}+(-3)^{2}}}$=6,解得m=±30.
∴满足条件的直线方程为:4x-3y±30=0.
(2)联立$\left\{\begin{array}{l}{2x+3y-5=0}\\{7x+15y+1=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{26}{3}}\\{y=-\frac{37}{9}}\end{array}\right.$.
设平行于直线 x+2y-3=0的直线方程为 x+2y+n=0.
把$\left\{\begin{array}{l}{x=\frac{26}{3}}\\{y=-\frac{37}{9}}\end{array}\right.$代入上述方程可得:n=-$\frac{4}{9}$.
∴要求的直线方程为:9x+18y-4=0.
点评 本题考查了相互平行与垂直的直线斜率之间的关系、直线的交点、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
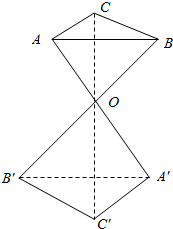 如图,△ABC和△A′B′C′的对应顶点的连线AA′,BB′,CC′交于同一点O,且$\frac{AO}{OA′}=\frac{BO}{OB′}=\frac{CO}{OC′}=\frac{2}{3}$.
如图,△ABC和△A′B′C′的对应顶点的连线AA′,BB′,CC′交于同一点O,且$\frac{AO}{OA′}=\frac{BO}{OB′}=\frac{CO}{OC′}=\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com