
下表中数阵为“森德拉姆素数筛”,其特点是每行每列都成等差数列,记第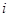 行第
行第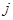 列的数为
列的数为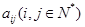 ,则:
,则:

(Ⅰ)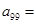 ; (Ⅱ)表中数
; (Ⅱ)表中数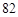 共出现 次.
共出现 次.
(Ⅰ)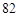 ,(Ⅱ)
,(Ⅱ)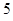
【解析】
试题分析:利用观察法及定义可知第1行数组成的数列A1j(j=1,2,)是以2为首项,公差为1的等差数列,进一步分析得知第j列数组成的数列A1j(i=1,2,)是以j+1为首项,公差为j的等差数列,同时分别求出通项公式,从而从而得知结果。
第i行第j列的数记为Aij.那么每一组i与j的解就是表中一个数.
因为第一行数组成的数列A1j(j=1,2,)是以2为首项,公差为1的等差数列,
所以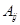 =2+(j-1)×1=j+1,
=2+(j-1)×1=j+1,
所以第j列数组成的数列A1j(i=1,2,)是以j+1为首项,公差为j的等差数列,
所以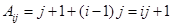
令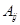 =ij+1=2010,故可知
=ij+1=2010,故可知
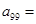 82,表中数
82,表中数 +1=82,
+1=82,
 =81=
=81= ,共出现了5次。
,共出现了5次。
考点:等差数列
点评:此题考查行列模型的等差数列的求法,运用所学的等差数列和等比数列来求解通项公式是解题的关键,属于中档题。


科目:高中数学 来源: 题型:
| 2 | 3 | 4 | 5 | 6 | 7 | … |
| 3 | 5 | 7 | 9 | 11 | 13 | … |
| 4 | 7 | 10 | 13 | 16 | 19 | … |
| 5 | 9 | 13 | 17 | 21 | 25 | … |
| 6 | 11 | 16 | 21 | 26 | 31 | … |
| 7 | 13 | 19 | 25 | 31 | 37 | … |
| … | … | … | … | … | … | … |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省武汉市高三11月调考理科数学试卷(解析版) 题型:填空题
下表中的数阵为“森德拉姆素数筛”,其特点是每行每列都成等差数列,记第i行第j列的数为ai,j(i,j∈N*),则

(Ⅰ)a9,9= ;
(Ⅱ)表中的数82共出现 次.
查看答案和解析>>
科目:高中数学 来源: 题型:
下表中的数阵为“森德拉姆素数筛”,其特点是每行每列都成等差数列,记第i行第j列的数为ai,j(i,j∈N*),则
(Ⅰ)a9,9= ;
(Ⅱ)表中的数82共出现 次.
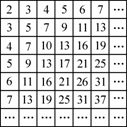
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com