
【题目】已知a∈R,命题p:x∈[-2,-1],x2-a≥0,命题q:![]() .
.
(1)若命题p为真命题,求实数a的取值范围;
(2)若命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)令f(x)=x2-a,可将问题转化为“当![]() 时,
时,![]() ”,故求出
”,故求出![]() 即可.(2)根据“p∨q”为真命题,命题“p∧q”为假命题可得p与q一真一假,然后分类讨论可得所求的结果.
即可.(2)根据“p∨q”为真命题,命题“p∧q”为假命题可得p与q一真一假,然后分类讨论可得所求的结果.
(1)令![]() ,
,
根据题意,“命题p为真命题”等价于“当![]() 时,
时,![]() ”.
”.
∵![]() ,
,
∴![]() ,
,
解得![]() .
.
∴实数![]() 的取值范围为
的取值范围为![]() .
.
(2)由(1)可知,当命题p为真命题时,实数![]() 满足
满足![]() .
.
当命题q为真命题,即方程有实数根时,则有Δ=4a2-4(2-a)≥0,
解得![]() 或
或![]() .
.
∵命题“p∨q”为真命题,命题“p∧q”为假命题,
∴命题p与q一真一假
①当命题p为真,命题q为假时,
得![]() ,解得
,解得![]() ;
;
②当命题p为假,命题q为真时,
得![]() ,解得
,解得![]() .
.
综上可得![]() 或
或![]() .
.
∴实数![]() 的取值范围为
的取值范围为![]() .
.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
【题目】已知有一个三边长分别为3,4,5的三角形.求下面两只蚂蚁与三角形三顶点的距离均超过1的概率.(1)一只蚂蚁在三角形的边上爬行(2)一只蚂蚁在三角形所在区域内部爬行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABO﹣A1B1O1中,侧面AOO1A1与侧面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1 , OB=3,O1B1=1,OO1= ![]() .
. 
(1)证明:AB1⊥BO1;
(2)求直线AO1与平面AOB1所成的角的正切值;
(3)求二面角O﹣AB1﹣O1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABO﹣A1B1O1中,侧面AOO1A1与侧面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1 , OB=3,O1B1=1,OO1= ![]() .
. 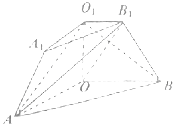
(1)证明:AB1⊥BO1;
(2)求直线AO1与平面AOB1所成的角的正切值;
(3)求二面角O﹣AB1﹣O1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣lnx(a∈R)
(1)当a=1时,求函数y=f(x)的单调区间;
(2)若x∈(0,1],|f(x)|≥1恒成立,求a的取值范围;
(3)若a= ![]() ,证明:ex﹣1f(x)≥x.
,证明:ex﹣1f(x)≥x.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左右焦点分别
的左右焦点分别![]()
![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆于
交椭圆于![]() 两点,满足
两点,满足![]() .
.
(1)求椭圆![]() 的离心率.
的离心率.
(2)![]() 是椭圆
是椭圆![]() 短轴的两个端点,设点
短轴的两个端点,设点![]() 是椭圆
是椭圆![]() 上一点(异于椭圆
上一点(异于椭圆![]() 的顶点),直线
的顶点),直线![]() 分别与
分别与![]() 轴相交于
轴相交于![]() 两点,
两点,![]() 为坐标原点,若
为坐标原点,若![]() ,求椭圆
,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=e|lnx|(e为自然对数的底数).若x1≠x2且f(x1)=f(x2),则下列结论一定不成立的是( )
A.x2f(x1)>1
B.x2f(x1)=1
C.x2f(x1)<1
D.x2f(x1)<x1f(x2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=﹣an﹣( ![]() )n﹣1+2(n∈N*),数列{bn}满足bn=2nan .
)n﹣1+2(n∈N*),数列{bn}满足bn=2nan .
(Ⅰ)求证数列{bn}是等差数列,并求数列{an}的通项公式;
(Ⅱ)设cn=log2 ![]() ,数列{
,数列{ ![]() }的前n项和为Tn , 求满足Tn
}的前n项和为Tn , 求满足Tn ![]() (n∈N*)的n的最大值.
(n∈N*)的n的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com