练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，将四棱锥S-ABCD的每一个顶点染上一种颜色，并使同一条棱的两端点异色.如果只有5种不同的颜色可供选择，那么不同的染色方法共有多少种?

    解析：将四棱锥S-ABCD沿侧棱剪开展在同一平面上(如图)，

    由题设知，点S，A，B所染色互不相同，它们共有5×4×3=60种不同的染色方法.为叙述方便，把5种不同的颜色分别记为1，2，3，4，5.当S，A，B染好色后，不妨设它们分别染色为1，2，3.若C染色2，则D可染3，4，5中的任一种色，有3种染法；若C染色4，则D可染3或5，有2种染法；若C染色5，则D可染3或4，也有2种染法.根据分步原理，总的染色方法有N=60×(3+2+2)=420(种).

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

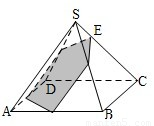
    （2012•江西）如图，已知正四棱锥S-ABCD所有棱长都为1，点E是侧棱SC上一动点，过点E垂直于SC的截面将正四棱锥分成上、下两部分．记SE=x（0＜x＜1），截面下面部分的体积为V（x），则函数y=V（x）的图象大致为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一块边长为10的正方形纸片，按如图所示将阴影部分裁下，然后将余下的四个全等的等腰三角形作为侧面制作一个正四棱锥S-ABCD（底面是正方形，顶点在底面的射影是底面中心的四棱锥）．
    （1）过此棱锥的高以及一底边中点F作棱锥的截面（如图），设截面三角形面积为y，求y的最大值及y取最大值时的x的值；
    （2）空间一动点P满足
    SP
    =a
    SA
    +b
    SB
    +c
    SC
    （a+b+c=1），在第（1）问的条件下，求|
    SP
    |    的最小值，并求取得最小值时a，b，c的值；
    （3）在第（1）问的条件下，设F是CD的中点，问是否存在这样的动点Q，它在此棱锥的表面（包含底面ABCD）运动，且FQ⊥AC？如果存在，计算其运动轨迹的长度，如果不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年四川省成都市树德中学高二（上）期中数学试卷（理科）（解析版） 题型：解答题

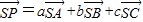    一块边长为10的正方形纸片，按如图所示将阴影部分裁下，然后将余下的四个全等的等腰三角形作为侧面制作一个正四棱锥S-ABCD（底面是正方形，顶点在底面的射影是底面中心的四棱锥）．
    （1）过此棱锥的高以及一底边中点F作棱锥的截面（如图），设截面三角形面积为y，求y的最大值及y取最大值时的x的值；
    （2）空间一动点P满足（a+b+c=1），在第（1）问的条件下，求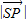的最小值，并求取得最小值时a，b，c的值；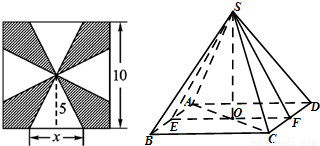
    （3）在第（1）问的条件下，设F是CD的中点，问是否存在这样的动点Q，它在此棱锥的表面（包含底面ABCD）运动，且FQ⊥AC？如果存在，计算其运动轨迹的长度，如果不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年福建省莆田四中高二（上）辅优周练数学试卷（二）（解析版） 题型：选择题

    如图，已知正四棱锥S-ABCD所有棱长都为1，点E是侧棱SC上一动点，过点E垂直于SC的截面将正四棱锥分成上、下两部分．记SE=x（0＜x＜1），截面下面部分的体积为V（x），则函数y=V（x）的图象大致为（ ）

    A．
    B．
    C．
    D．

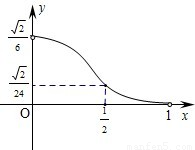
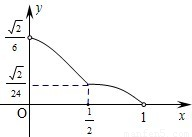
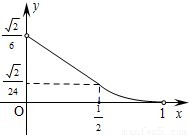
    查看答案和解析>>

    科目：高中数学 来源：2012年江西省高考数学试卷（理科）（解析版） 题型：选择题

    如图，已知正四棱锥S-ABCD所有棱长都为1，点E是侧棱SC上一动点，过点E垂直于SC的截面将正四棱锥分成上、下两部分．记SE=x（0＜x＜1），截面下面部分的体积为V（x），则函数y=V（x）的图象大致为（ ）

    A．
    B．
    C．
    D．

    查看答案和解析>>

    同步练习册答案