
 轴右侧的圆C与
轴右侧的圆C与 相切于点P(0,1),与
相切于点P(0,1),与 轴相交于点A、B,且被
轴相交于点A、B,且被 轴分成的两段弧之比为1﹕2(如图所示).
轴分成的两段弧之比为1﹕2(如图所示). 与圆C相交于点E、F,且以线段EF为直径的圆恰好过圆心C,求直线
与圆C相交于点E、F,且以线段EF为直径的圆恰好过圆心C,求直线 的方程.
的方程.
 轴右侧,且与
轴右侧,且与 相切于点P(0,1),
相切于点P(0,1),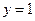 上.
上. 轴分成的两段弧之比为1﹕2,所以
轴分成的两段弧之比为1﹕2,所以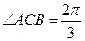 . ……………………….3分
. ……………………….3分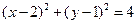 . ……………………………………………6分(II)①若直线
. ……………………………………………6分(II)①若直线 斜率存在,设直线
斜率存在,设直线 的方程为
的方程为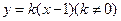 ,即
,即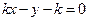 .
.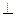 FC.
FC. . …………………………………………………………………8分
. …………………………………………………………………8分 的距离
的距离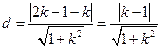 .
.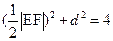 得
得 .
.  的方程为
的方程为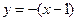 ,即
,即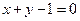 . ………………………11分
. ………………………11分 斜率不存在,此时直线
斜率不存在,此时直线 的方程为
的方程为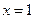 ,点E、F的坐标分别为
,点E、F的坐标分别为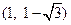 、
、 ,可以验证不满足条件. …………………………………………..13分
,可以验证不满足条件. …………………………………………..13分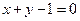 . ……………………………………14分
. ……………………………………14分

 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源:不详 题型:填空题

 和
和 ,第一排和最后一排的距离
,第一排和最后一排的距离 米(如图所示),旗杆底部与第一排在一个水平面上.
米(如图所示),旗杆底部与第一排在一个水平面上. 秒,升旗手应以 (米 /秒)的速度匀速升旗.
秒,升旗手应以 (米 /秒)的速度匀速升旗.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com