解:(1)列表:
| x |  | 2π | 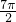 | 5π | 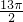 |
 x- x- | 0 |  | π |  | 2π |
y=2sin( - - ) ) | 0 | 2 | 0 | -2 | 0 |
画图,如图所示:
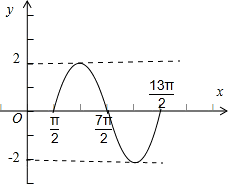
(2)此函数的振幅A=2,周期为 T=
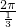
=6π,频率为
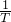
=
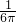
,初相为-

.
由

x-

=kπ,解得 x=3kπ+

,k∈z,故函数的对称中心为(3kπ+

,0),k∈z.
(3)由于函数y=2sin(
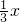
-

)=2sin[

(x-

)],
故把函数y=2sin(
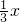
-

)的图象向左平移

个单位可得函数y=2sin[

(x+

-

)]=2sin

x的图象.
再把所得图象上各的横坐标变为原来的3倍,即可得到函数y=2sinx的图象,
再把所得图象上的各个点的纵坐标变为原来的一半,即得函数y=sinx的图象.
分析:(1)根据函数的解析式列表,用五点法做出图象.
(2)根据函数y=Asin(ωx+∅)的振幅、周期、频率、初相的定义,求得结论,令由

x-

=kπ,解得 x的值,
可得函数y=Asin(ωx+∅)的对称中心的坐标.
(3)依据函数y=Asin(ωx+∅)的图象变换规律,得出结论.
点评:本题主要考查用五点法做函数y=Asin(ωx+∅)的图象,振幅、周期、频率、初相的定义,函数y=Asin(ωx+∅)的对称
中心,以及函数y=Asin(ωx+∅)的图象变换规律,属于中档题.

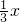 -
- ).
).
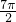
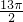
 x-
x-


 -
- )
)
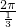 =6π,频率为
=6π,频率为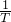 =
=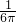 ,初相为-
,初相为- .
. x-
x- =kπ,解得 x=3kπ+
=kπ,解得 x=3kπ+ ,k∈z,故函数的对称中心为(3kπ+
,k∈z,故函数的对称中心为(3kπ+ ,0),k∈z.
,0),k∈z.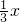 -
- )=2sin[
)=2sin[ (x-
(x- )],
)],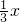 -
- )的图象向左平移
)的图象向左平移 个单位可得函数y=2sin[
个单位可得函数y=2sin[ (x+
(x+ -
- )]=2sin
)]=2sin x的图象.
x的图象. x-
x- =kπ,解得 x的值,
=kπ,解得 x的值,

 下列4个命题:
下列4个命题: