
分析 分析题目中的要求,发现这是一个累加型的问题,用循环语句来实现,累加的初始值为0,累加值每一次增加1/n,退出循环的条件是累加结果>10,把握住以上要点不难得到程序框图,从而写出程序.
解答 解:S=0
n=1
WHILE S<=10
S=S+1/n
n=n+1
WEND
PRINT n-1
END
点评 可利用循环语句来实现数值的累加(乘)常分如下步骤:①观察S的表达式分析,循环的初值、终值、步长②观察每次累加的值的通项公式③在循环前给累加器和循环变量赋初值,累加器的初值为0,累乘器的初值为1,环变量的初值同累加(乘)第一项的相关初值④在循环体中要先计算累加(乘)值,如果累加(乘)值比较简单可以省略此步,累加(乘),给循环变量加步长⑤输出累加(乘)值.


科目:高中数学 来源: 题型:解答题
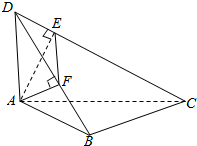 如图,在空间四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB.
如图,在空间四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-3=0 | B. | 2x-y-5=0 | C. | 2x+y=0 | D. | x-y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P(x,y,z)中x,y,z的位置可以互换的 | |
| B. | 空间直角坐标系中的点与一个三元有序数组是一种一一对应关系 | |
| C. | 空间直角坐标系中的三条坐标轴把空间分成八个部分 | |
| D. | 某点在不同空间直角坐标系中的坐标位置可以相同 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等于$\frac{4}{3}$ | B. | 等于$\frac{3}{4}$ | C. | 等于$\frac{8}{3}$ | D. | 有很多种情况 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3-i | B. | 2-3i | C. | 3+i | D. | 2+3i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com