
分析 由销售价格为3元/件时,每日可售出该商品11件,建立方程,求出a,可得f(x)的解析式;商场每日销售该商品所获得的利润=每日的销售量×销售该商品的单利润,可得日销售量的利润函数为关于x的三次多项式函数,再用求导数的方法讨论函数的单调性,得出函数的极大值点,从而得出最大值对应的x值.
解答 解:由题意,销售价格为3元/件时,每日可售出该商品11件,
∴11=$\frac{480+a}{3-1}$+10×9-80×3,解得a=-158,故y=$\frac{160x-158}{x-1}$+10x2-80x(1<x<4);
商场每日销售该商品所获得的利润为g(x)=(x-1)f(x)=(160x-158)+(x-1)(10x2-80x)(1<x<4),
g′(x)=30(x-4)(x-2).
列表得x,y,y′的变化情况:
| x | (1,2) | 2 | (2,4) |
| g′(x) | + | 0 | - |
| g(x) | 单调递增 | 极大值42 | 单调递减 |
点评 本题函数解析式的建立比较容易,考查的重点是利用导数解决生活中的优化问题,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
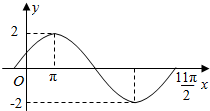 已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$图象的一部分如图所示.
已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$图象的一部分如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | [-2,1] | C. | (-∞,-2)∪(1,+∞) | D. | (-2,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com