
 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.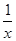 的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.
的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围. ,
, 解得-1≤a≤1.
解得-1≤a≤1.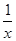 得x2-ax-2=0.
得x2-ax-2=0.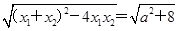 ,因为a∈[-1,1],所以
,因为a∈[-1,1],所以 ≤3,即|x1-x2|max=3,
≤3,即|x1-x2|max=3,


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源:不详 题型:解答题
 与时间
与时间 小时
小时 间的关系为
间的关系为 .如果在前
.如果在前 个小时消除了
个小时消除了 的污染物,试求:
的污染物,试求: 个小时后还剩百分之几的污染物?
个小时后还剩百分之几的污染物?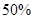 所需要的时间.(参考数据:
所需要的时间.(参考数据: )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 对任意的
对任意的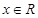 恒有
恒有 成立.
成立. 若
若 在
在 )上为增函数,求c的取值范围;
)上为增函数,求c的取值范围; 时,
时, 成立;
成立; 恒成立,求M的最小值.
恒成立,求M的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.m+n<0 | B.m+n>0 |
| C.m-n<0 | D.m-n>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com