
 对任意的
对任意的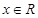 恒有
恒有 成立.
成立. 若
若 在
在 )上为增函数,求c的取值范围;
)上为增函数,求c的取值范围; 时,
时, 成立;
成立; 恒成立,求M的最小值.
恒成立,求M的最小值.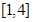 ;(2)证明见解析;(3)
;(2)证明见解析;(3)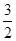 .
.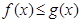 对
对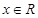 恒成立,
恒成立,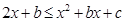 ,即
,即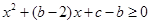 恒成立,这是二次不等式,由二次函数知识,有
恒成立,这是二次不等式,由二次函数知识,有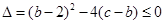 ,化简之后有
,化简之后有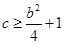 ,从而
,从而 .
.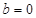 时,
时,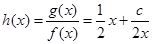 在
在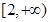 上是增函数,我们用增函数的定义,即设
上是增函数,我们用增函数的定义,即设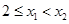 ,
,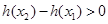 恒成立,分析后得出
恒成立,分析后得出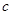 的范围;(2)
的范围;(2)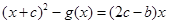
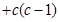 ,问题变成证明
,问题变成证明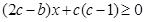 在
在 时恒成立,在
时恒成立,在 的情况下,
的情况下,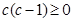 ,而
,而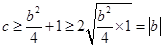 ,可见
,可见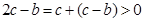 ,那当
,那当 时,一定恒有
时,一定恒有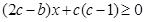 ,问题证毕;(3)由(2)
,问题证毕;(3)由(2)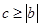 ,在
,在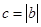 时,
时,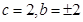 ,这时柺验证不等式
,这时柺验证不等式 成立,当
成立,当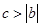 时
时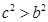 ,不等式可化为
,不等式可化为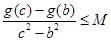 ,因此要求
,因此要求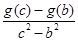 的最大值或者它的值域,
的最大值或者它的值域,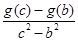
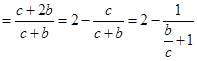 ,而
,而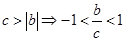 ,因此
,因此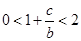 ,由此
,由此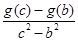 的取值范围易得,
的取值范围易得,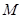 的最小值也易得.
的最小值也易得.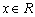 恒有
恒有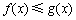 成立,
成立, 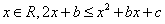 ,即
,即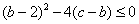 恒成立.
恒成立. 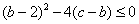 ,从而
,从而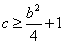 .,即:
.,即: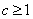 .
. 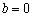 时,记
时,记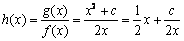 (
(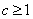 )
) 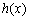 在
在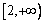 上为增函数,所以任取
上为增函数,所以任取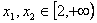 ,
,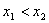 ,
, 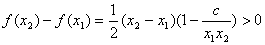 恒成立.
恒成立. 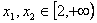 ,
,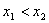 ,
,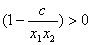 成立,也就是
成立,也就是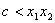 成立.
成立. 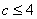 ,即
,即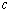 的取值范围是
的取值范围是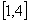 .
. 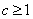 且
且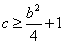 ,
, 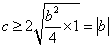 ,因此
,因此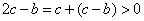 .
.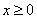 时,有
时,有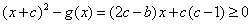 .
.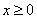 时,
时,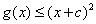 .
.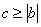 ,
, 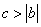 时,有
时,有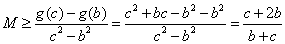
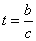 ,则
,则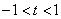 ,
, 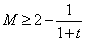 ,由于
,由于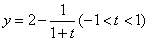 的值域为
的值域为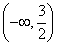 ,
, 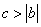 时,
时,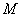 的取值范围是
的取值范围是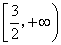 ;
; 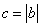 时,由(1)知,
时,由(1)知,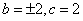 .此时
.此时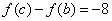 或0,
或0,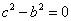 ,
,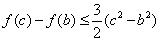 恒成立.
恒成立.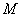 的最小值为
的最小值为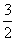 .
. 

科目:高中数学 来源:不详 题型:解答题
 ,若存在非零常数
,若存在非零常数 ,使函数
,使函数 对于定义域内的任意实数
对于定义域内的任意实数 ,都有
,都有 ,则称函数
,则称函数 是广义周期函数,其中称
是广义周期函数,其中称 为函数
为函数 的广义周期,
的广义周期, 称为周距.
称为周距. 是以2为广义周期的广义周期函数,并求出它的相应周距
是以2为广义周期的广义周期函数,并求出它的相应周距 的值;
的值; ,使
,使 (
( 为常数,
为常数, )为广义周期函数,并求出它的一个广义周期
)为广义周期函数,并求出它的一个广义周期 和周距
和周距 ;
; 是周期
是周期 的周期函数,当函数
的周期函数,当函数 在
在 上的值域为
上的值域为 时,求
时,求 在
在 上的最大值和最小值.
上的最大值和最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.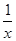 的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.
的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 =________.
=________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com