
【题目】已知函数![]() ,
,![]() .
.
(1)求证:存在唯一的实数![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 相切;
相切;
(2)若![]() ,
,![]() ,求证:
,求证:![]() .
.
(注:![]() 为自然对数的底数.)
为自然对数的底数.)
【答案】(1)见解析;(2)见解析
【解析】
(1)曲线![]() 在
在![]() 处的切线为
处的切线为![]() ,所以
,所以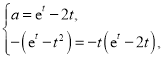 只需证明
只需证明![]() 有唯一解即可.
有唯一解即可.
(2) 要证![]() ,即证
,即证![]() ,设
,设![]() ,即
,即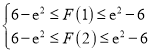 ,只要证明
,只要证明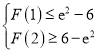 ,然后构造函数,讨论单调性,分析函数的最值,即可证明.
,然后构造函数,讨论单调性,分析函数的最值,即可证明.
证明:(1)由![]() 知,在
知,在![]() 处的切线为
处的切线为![]() ,
,
当该直线为![]() 时,可得
时,可得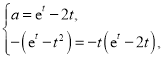
所以![]() ,所以
,所以![]() ,
,
令![]() ,则当
,则当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递增,
单调递增,
而![]() ,
,![]() ,所以存在唯一的实数
,所以存在唯一的实数![]() (
(![]() ),
),
使得![]() ,相应的
,相应的![]() 也是唯一的,
也是唯一的,
即存在唯一-的实数![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 相切.
相切.
(2)要证![]() ,即证
,即证![]() ,
,
令![]() ,对于确定的
,对于确定的![]() ,
,![]() 是一次函数,只要证明,
是一次函数,只要证明,
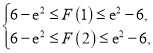
注意到对于同一![]() ,
,![]() ,所以只要证明
,所以只要证明

先证明①:记![]() ,则
,则![]() ,
,
令![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
由此可知![]() 在区间
在区间![]() 递减,在区间
递减,在区间![]() 递增.
递增.
又因为![]() ,
,![]() ,
,![]() ,
,
所以,在区间![]() 上存在唯一实数
上存在唯一实数![]() ,使得
,使得![]() .
.
故在区间![]() ,
,![]() 递减,在区间
递减,在区间![]() ,
,![]() 递增.
递增.
于是![]() .①得证.
.①得证.
再证明②:记![]() ,
,
当![]() 时,利用不等式
时,利用不等式![]() 得,
得,
![]() ;
;
当![]() 时,利用不等式
时,利用不等式![]() (
(![]() )得
)得
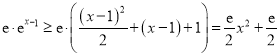 ,
,
于是![]() ,
,
其中二次函数![]() 开口向上,对称轴为
开口向上,对称轴为![]() ,
,
当![]() 时,
时,![]() 最小值为
最小值为![]() ,
,
所以![]() .
.
综上,不等式①②均成立.
所以,当![]() ,对任意的
,对任意的![]() ,总有
,总有![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以![]() 再加1;如果它是偶数,则将它除以
再加1;如果它是偶数,则将它除以![]() ;如此循环,最终都能够得到
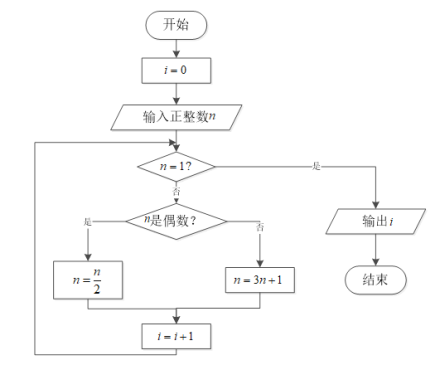
;如此循环,最终都能够得到![]() .下图为研究“角谷猜想”的一个程序框图.若输入
.下图为研究“角谷猜想”的一个程序框图.若输入![]() 的值为
的值为![]() ,则输出i的值为( )
,则输出i的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过原点
,过原点![]() 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆![]() 交于点
交于点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 、
、![]() .
.
(1)若![]() ,求点
,求点![]() 的横坐标;
的横坐标;
(2)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中心在原点的椭圆E的一个焦点与抛物线![]() 的焦点关于直线
的焦点关于直线![]() 对称,且椭圆E与坐标轴的一个交点坐标为
对称,且椭圆E与坐标轴的一个交点坐标为![]() .
.
(1)求椭圆E的标准方程;
(2)过点![]() 的直线l(直线的斜率k存在且不为0)交E于A,B两点,交x轴于点P点A关于x轴的对称点为D,直线BD交x轴于点Q.试探究
的直线l(直线的斜率k存在且不为0)交E于A,B两点,交x轴于点P点A关于x轴的对称点为D,直线BD交x轴于点Q.试探究![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】工厂质检员从生产线上每半个小时抽取一件产品并对其某个质量指标![]() 进行检测,一共抽取了
进行检测,一共抽取了![]() 件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标
件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标![]() 有关,具体见下表.
有关,具体见下表.
质量指标 |
|
|
|
频数 |
|
|
|
一年内所需维护次数 |
|
|
|
(1)以每个区间的中点值作为每组指标的代表,用上述样本数据估计该厂产品的质量指标![]() 的平均值(保留两位小数);
的平均值(保留两位小数);
(2)用分层抽样的方法从上述样本中先抽取![]() 件产品,再从
件产品,再从![]() 件产品中随机抽取
件产品中随机抽取![]() 件产品,求这
件产品,求这![]() 件产品的指标
件产品的指标![]() 都在
都在![]() 内的概率;
内的概率;
(3)已知该厂产品的维护费用为![]() 元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加
元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加![]() 元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这
元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这![]() 件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )

A. 甲的极差是29 B. 甲的中位数是24
C. 甲罚球命中率比乙高 D. 乙的众数是21
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】试研究,一个三角形能否同时具有以下两个性质:(1)三边是连续的三个自然数;(2)最大角是最小角的2倍.若能,请求出这个三角形的三边以及最大角的余弦值;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() 的左右两个焦点,过
的左右两个焦点,过![]() 的直线与
的直线与![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 在第一象限),
在第一象限),![]() 的周长为8,
的周长为8,![]() 的离心率为
的离心率为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() ,
,![]() 为
为![]() 的左右顶点,直线
的左右顶点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,已知椭圆C:![]() 的离心率为
的离心率为![]() ,且点
,且点![]() 在椭圆C上.椭圆C的左顶点为A.
在椭圆C上.椭圆C的左顶点为A.
(1)求椭圆C的方程
(2)椭圆的右焦点且斜率为![]() 的直线与椭圆交于P,Q两点,求三角形APQ的面积;
的直线与椭圆交于P,Q两点,求三角形APQ的面积;
(3)过点A作直线与椭圆C交于另一点B.若直线![]() 交
交![]() 轴于点C,且
轴于点C,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com