
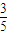 ),则P(ξ=偶数)+P(ξ=奇数)=1,再根据二项式定理求出P(ξ=偶数)-P(ξ=奇数)的值,从而求出P(ξ=奇数)的值.
),则P(ξ=偶数)+P(ξ=奇数)=1,再根据二项式定理求出P(ξ=偶数)-P(ξ=奇数)的值,从而求出P(ξ=奇数)的值.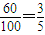
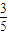 ),P(ξ=k)=
),P(ξ=k)=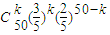 ,k=0,1,2,3…50.
,k=0,1,2,3…50.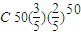 +
+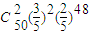 +…+
+…+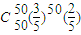 ]-[
]-[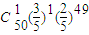 +
+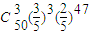 +…+
+…+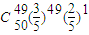 ]
]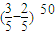 =
=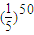 …由此可得P(ξ=奇数)=
…由此可得P(ξ=奇数)= [1-
[1-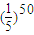 ]
] [1-
[1-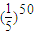 ]
]

科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:2004年广东省深圳市松岗中学高考数学模拟试卷(2)(解析版) 题型:解答题
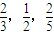
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com