
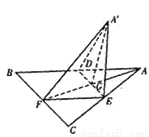
如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列四个命题:
①动点A′在平面ABC上的射影在线段AF上;
②恒有平面A′GF⊥平面BCED;
③三棱锥A′—FED的体积有最大值;
④异面直线A′E与BD不可能互相垂直;
其中正确命题的序号是 .
①②③
【解析】
试题分析:过A′作A'H⊥面ABC,垂足为H,因为△ABC为正三角形且中线AF与中位线DE相交,所以AG⊥DE A′G⊥DE,又因为AG∩A′G=G,所以DE⊥面A′GA,
因为DE⊂面ABC,所以面A′GF⊥面ABC且面A′GA∩面ABC=AF
所以H在AF上,故恒有平面A′GF⊥平面BCED,故①对③对.
S三棱锥A′-FED=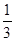 S△EFD•A′H,因为底面面积是个定值,所以当A′H为A′G时,三棱锥的面积最大,故②对;在△A′ED是△AED绕DE旋转的过程中异面直线A′E与BD可能互相垂直,故④不对故答案为:(1)(2)(3).
S△EFD•A′H,因为底面面积是个定值,所以当A′H为A′G时,三棱锥的面积最大,故②对;在△A′ED是△AED绕DE旋转的过程中异面直线A′E与BD可能互相垂直,故④不对故答案为:(1)(2)(3).
考点:本题考查平空间中点、线、面的位置关系;线面、面面垂直的判定定理与性质定理;异面直线所成的角;命题真假的判断。
点评:此类题型一般涉及多个知识点,综合性较强,但难度不大。对于错误的命题举出反例即可.


科目:高中数学 来源: 题型:
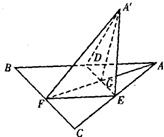 如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题:①动点A′在平面ABC上的射影在线段AF上;②三棱锥A′-FED的体积有最大值;③恒有平面A′GF⊥平面BCED;
如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题:①动点A′在平面ABC上的射影在线段AF上;②三棱锥A′-FED的体积有最大值;③恒有平面A′GF⊥平面BCED;| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有
如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有查看答案和解析>>
科目:高中数学 来源:2011届山东省济宁一中高三第三次月考理科数学卷 题型:填空题
如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有 .
①动点A′在平面ABC上的射影在线段AF上;
②三棱锥A′—FED的体积有最大值;
③恒有平面A′GF⊥平面BCED;
④异面直线A′E与BD不可能互相垂直;
⑤异面直线FE与A′D所成角的取值范围是
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省高三第三次月考理科数学卷 题型:填空题
如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有 .

①动点A′在平面ABC上的射影在线段AF上;
②三棱锥A′—FED的体积有最大值;
③恒有平面A′GF⊥平面BCED;
④异面直线A′E与BD不可能互相垂直;
⑤异面直线FE与A′D所成角的取值范围是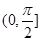
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com