对n∈N*,定义函数fn(x)=-(x-n)2+n,n-1≤x≤n.
(1)求证:y=fn(x)图象的右端点与y=fn+1(x)图象的左端点重合;并回答这些端点在哪条直线上.
(2)若直线y=knx与函数fn(x)=-(x-n)2+n,n-1≤x≤n(n≥2,n∈N*)的图象有且仅有一个公共点,试将kn表示成n的函数.
(3)对n∈N*,n≥2,在区间[0,n]上定义函数y=f(x),使得当m-1≤x≤m(n∈N*,且m=1,2,…,n)时,f(x)=fm(x).试研究关于x的方程f(x)=fn(x)(0≤x≤n,n∈N*)的实数解的个数(这里的kn是(2)中的kn),并证明你的结论.
【答案】
分析:(1)由f
n(n)=n 得 y=f
n(x)图象右端点的坐标为(n,n),由f
n+1(n)=n得 y=f
n+1(x)图象左端点的坐标为(n,n),故两端点重合,且这些点在直线y=x上.
(2)由题设及(1)的结论方程-(x-n)
2+n=k
n•x可得 1<k
n<2,且k
n单调递减.在n-1≤x≤n上有两个相等的实数根.求出方程的两个根,求得 k
n=2n-2
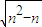
,
(n≥2,n∈N
*).
(3)当n≥2时,求得 k
n=
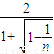
,可得 1<k
n<2,且k
n单调递减.分①当n≥3时,和②当n=2时两种情况,分别求得方程 f(x)=k
n•x( 0≤x≤n,n∈N
*)的实数解的
个数为2n-1,从而证得结论.
解答:(1)证明:由f
n(n)=n 得 y=f
n(x)图象右端点的坐标为(n,n),
由f
n+1(n)=n得 y=f
n+1(x)图象左端点的坐标为(n,n),故两端点重合. (2分)
并且对 n∈N
*,这些点在直线y=x上.(4分)
(2)由题设及(1)的结论,两个函数图象有且仅有一个公共点,即方程-(x-n)
2+n=k
n•x在 满足n-1≤x≤n的区间上有两个相等的实数根.
整理方程得 x
2+(k
n-2n)x+n
2-n=0,
由△=
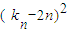
-4(n
2-n)=0,解得 k
n=2n±2
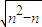
,(8分)
此时方程的两个实数根x
1,x
2相等,由 x
1+x
2=2n-k
n,
得 x
1=x
2=
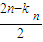
=[2n±2
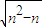
]=m
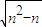
,
因为 n-1≤x
1=x
2≤n,所以只能 k
n=2n-2
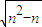
,(n≥2,n∈N
*).(10分)
(3)当n≥2时,求得 k
n=2n-2
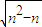
=
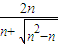
=
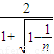
,
可得 1<k
n<2,且k
n单调递减. (14分)
①当n≥3时,对于2≤i≤n-1,总有1<k
n<k
i,亦即直线y=k
nx与函数f
i(x)的图象总有两个不同的公共点(直线y=k
nx在直线y=x与直线y=k
i x之间).
对于函数f
i(x)来说,因为 1<k
n<2,所以方程 k
n•x=f
i(x)有两个解:x
1=0,x
2=2-k
n∈(0,1).
此时方程f(x)=k
n•x( 0≤x≤n,n∈N
*)的实数解的个数为2(n-1)+1=2n-1.(16分)
②当n=2时,因为1<k
2<2,所以方程 k
2x=f
i(x)有两个解.此时方程f(x)=k
2x.
(0≤x≤2)的实数解的个数为3. (17分)
综上,当n≥2,n∈N
*时,方程 f(x)=k
n•x( 0≤x≤n,n∈N
*)的实数解的个数为2n-1. (18分)
点评:本题主要考查函数的零点与方程的根的关系,二次函数的性质,体现了化归与转化的数学思想,属于中档题.

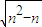 ,
,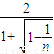 ,可得 1<kn<2,且kn单调递减.分①当n≥3时,和②当n=2时两种情况,分别求得方程 f(x)=kn•x( 0≤x≤n,n∈N*)的实数解的
,可得 1<kn<2,且kn单调递减.分①当n≥3时,和②当n=2时两种情况,分别求得方程 f(x)=kn•x( 0≤x≤n,n∈N*)的实数解的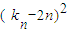 -4(n2-n)=0,解得 kn=2n±2
-4(n2-n)=0,解得 kn=2n±2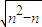 ,(8分)
,(8分)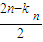 =[2n±2
=[2n±2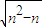 ]=m
]=m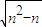 ,
,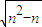 ,(n≥2,n∈N*).(10分)
,(n≥2,n∈N*).(10分)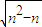 =
=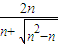 =
=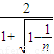 ,
,

 名校课堂系列答案
名校课堂系列答案