
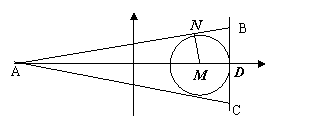
如图,已知点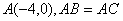 ,且
,且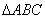 的内切圆方程为
的内切圆方程为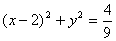 .
.
(1) 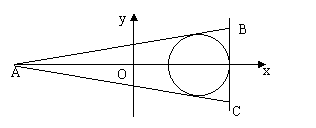 求经过
求经过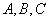 三点的椭圆标准方程;
三点的椭圆标准方程;
(2) 过椭圆上的点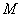 作圆的切线,求切线长最短时的点
作圆的切线,求切线长最短时的点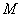 的坐标和切线长。
的坐标和切线长。
解:(Ⅰ)设椭圆的标准方程为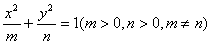 ,------------------1分
,------------------1分
依题意知直线AB的斜率存在,故设直线AB:y=k(x+4) ------------------2分
因圆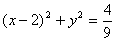 的圆心为(2,0),半径
的圆心为(2,0),半径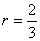 ,又因为直线AB与圆相切
,又因为直线AB与圆相切
所以,圆心为(2,0)到直线AB的距离为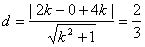 ------------------3分
------------------3分
解得 (
(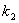 为直线AC的斜率)
为直线AC的斜率)
所以直线AB的方程为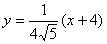 ,------------------4分
,------------------4分
又因为AB=AC,点A(-4,0)在x轴上,所以B点横坐标为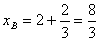 ,
,
把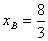 代入直线AB的方程解得
代入直线AB的方程解得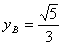 ,
,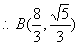 ------------------5分
------------------5分
把A(-4,0),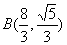 代入椭圆方程得
代入椭圆方程得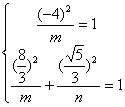 ,解得m=16,n=分
,解得m=16,n=分
所以椭圆的标准方程为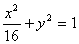 .------------------7分
.------------------7分
(Ⅱ)设点M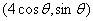 ,则圆心(2,0)与点M的距离为
,则圆心(2,0)与点M的距离为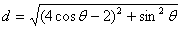 -8分
-8分
切线长 ,
,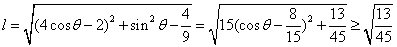 ,--10分
,--10分
当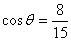 时,
时,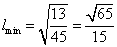 ,
------------------12分
,
------------------12分
此时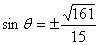 ,从而点
,从而点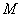 的坐标为
的坐标为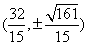 ------------------14分
------------------14分
解法二:(Ⅰ)因为AB=AC,点A(-4,0)在x轴上,且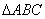 的内切圆方程为
的内切圆方程为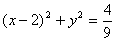 ,
,
 所以B点横坐标为
所以B点横坐标为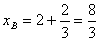 ,
-----------------1分
,
-----------------1分
如图,由三角形内切圆的性质知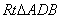 ∽
∽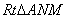
∴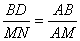 即
即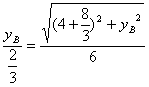 ,从而
,从而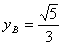
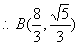 ------------------3分
------------------3分
当椭圆的焦点在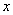 轴上时,设椭圆方程为
轴上时,设椭圆方程为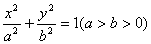 ,则将A(-4,0),
,则将A(-4,0),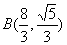 代入椭圆方程得
代入椭圆方程得 ,解得
,解得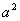 =16,
=16,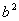 =1
,
=1
,
∴椭圆的标准方程为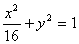 --5分
--5分
当椭圆的焦点在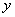 轴上时,设椭圆方程为
轴上时,设椭圆方程为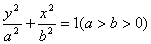 ,则将A(-4,0),
,则将A(-4,0),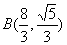 代入椭圆方程得
代入椭圆方程得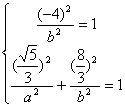 ,解得
,解得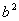 =16,
=16,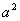 =
=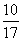 与
与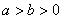 矛盾----------6分
矛盾----------6分
综上所述,所求椭圆的标准方程为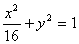 .------------------7分
.------------------7分
(Ⅱ) 依题意设点M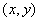 ,则圆心(2,0)与点M的距离为
,则圆心(2,0)与点M的距离为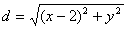 ------8分
------8分
则切线长 ,而
,而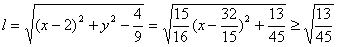 ,---------10分
,---------10分
当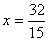 时,
时,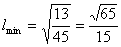 ,-----12分
,-----12分
此时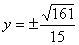 ,从而点
,从而点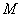 的坐标为
的坐标为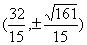 -----14分
-----14分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:

| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
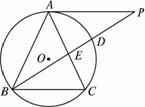
图17
A.![]() B.9 C.
B.9 C.![]() D.4
D.4
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省南京市高三第二次模拟考试数学卷 题型:解答题
在A、B、C、D四小题中只能选做2题,每小题10,共计20分。请在答题卡指定区域作答。解答应写出文字说明、证明过程或演算步骤。
A、选修4-1:几何证明选讲
如图,已知梯形ABCD为圆内接四边形,AD//BC,过C作该圆的切线,交AD的延长线于E,求证:ΔABC∽ΔEDC。

B、选修4-2:矩形与变换
已知 为矩阵
为矩阵 属于λ的一个特征向量,求实数a,λ的值及A2。
属于λ的一个特征向量,求实数a,λ的值及A2。
C、选修4-4:坐标系与参数方程
在平面直角坐标系xoy中,曲线C的参数方程为 (α为参数),曲线D的参数方程为
(α为参数),曲线D的参数方程为 ,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。
,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。
D、选修4-5:不等式选讲
已知a,b都是正实数,且ab=2。求证:(1+2a)(1+b)≥9。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山西省介休市高三下学期模拟考试理科数学 题型:解答题
(本小题满分12分)
如图,已知在坐标平面xOy内,M、N是x轴上关于原点O对称的两点,P是上半平面内一点,△PMN的面积为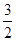 ,点A的坐标为(1+
,点A的坐标为(1+ ),
),  =m·
=m·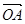 (m为常数),
(m为常数),



(1)求以M、N为焦点且过点P的椭圆方程;
(2)过点B(-1,0)的直线l交椭圆于C、D两点,交直线x=-4于点E,点B、E分 的比分别为λ1、λ2,求λ1+λ2的值。
的比分别为λ1、λ2,求λ1+λ2的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,已知椭圆C:![]() 的左右焦点分别为F1、F2,点B为椭圆与y轴的正半轴的交点,点P在第一象限内且在椭圆上,且PF2与x轴垂直,
的左右焦点分别为F1、F2,点B为椭圆与y轴的正半轴的交点,点P在第一象限内且在椭圆上,且PF2与x轴垂直,![]() (Ⅰ)求椭圆C的方程;
(Ⅰ)求椭圆C的方程;
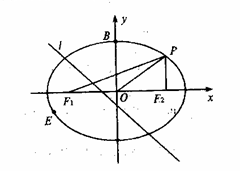 (Ⅱ)设点B关于直线
(Ⅱ)设点B关于直线![]() 的对称点E(异于点B)在椭圆C上,求m的值。
的对称点E(异于点B)在椭圆C上,求m的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com