Question

14．x∈R，用记号N（x）表示不小于实数的最小整数，例如N（2.5）=3，$N（{-\sqrt{2}}）=-1$，N（1）=1；则函数$f（x）=N（{3x+1}）-2x+\frac{1}{2}$的所有零点之和为-4．

Answer 1

分析 作函数y=3x+1与函数y=2x-$\frac{1}{2}$的图象，结合图象讨论以确定方程N（3x+1）=2x-$\frac{1}{2}$的解，从而求函数$f（x）=N（{3x+1}）-2x+\frac{1}{2}$的所有零点之和．

解答 解：作函数y=3x+1与函数y=2x-$\frac{1}{2}$的图象如下，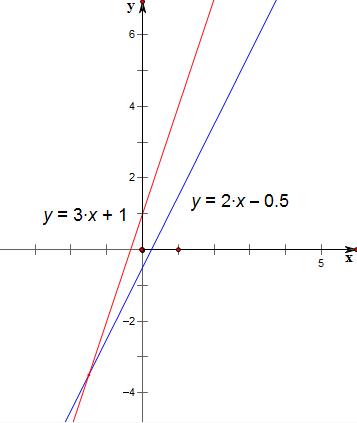

①当-4＜3x+1≤-3时，N（3x+1）=-3，故2x-$\frac{1}{2}$=-3，
解得，x=-$\frac{5}{4}$（舍去）；
②当-5＜3x+1≤-4时，N（3x+1）=-4，故2x-$\frac{1}{2}$=-4，
解得，x=-$\frac{7}{4}$；
③当-6＜3x+1≤-5时，N（3x+1）=-5，故2x-$\frac{1}{2}$=-5，
解得，x=-$\frac{9}{4}$；
④当-7＜3x+1≤-6时，N（3x+1）=-6，故2x-$\frac{1}{2}$=-6，
解得，x=-$\frac{11}{4}$（舍去）；
故函数$f（x）=N（{3x+1}）-2x+\frac{1}{2}$的所有零点之和为
-$\frac{7}{4}$-$\frac{9}{4}$=-4；
故答案为：-4．

点评 本题考查了数形结合的应用及分类讨论的思想应用，属于中档题．