
已知函数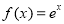 ,
,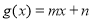 .
.
(1)设 .
.
① 若函数 在
在 处的切线过点
处的切线过点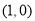 ,求
,求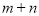 的值;
的值;
② 当 时,若函数
时,若函数 在
在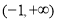 上没有零点,求
上没有零点,求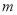 的取值范围;
的取值范围;
(2)设函数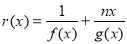 ,且
,且 ,求证:当
,求证:当 时,
时, .
.
(1)①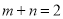 ,②
,②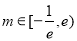 ,(2)详见解析
,(2)详见解析
【解析】
试题分析:(1)①利用导数几何意义求切线斜率: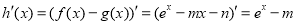 ,函数
,函数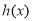 在
在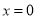 处的切线斜率
处的切线斜率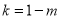 ,又
,又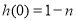 ,所以函数
,所以函数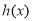 在
在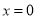 处的切线方程
处的切线方程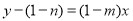 ,将点
,将点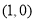 代入,得
代入,得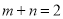 .②利用导数研究函数单调性,再根据函数单调性确定没有零点的条件:因为
.②利用导数研究函数单调性,再根据函数单调性确定没有零点的条件:因为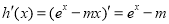 ,所以根据导函数有无零点分类讨论;当
,所以根据导函数有无零点分类讨论;当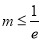 时,
时,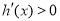 ,
,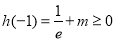 ,
,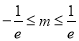 ;当
;当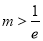 时,函数
时,函数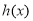 在
在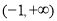 上有最小值为
上有最小值为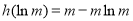 ,令
,令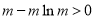 ,解得
,解得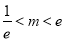 ;(2)由题意,
;(2)由题意,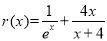 ,要确定其最小值,需多次求导,反复确定求单调性,最后确定
,要确定其最小值,需多次求导,反复确定求单调性,最后确定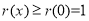
试题解析:(1)由题意,得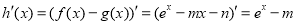 ,
,
所以函数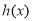 在
在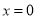 处的切线斜率
处的切线斜率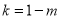 , 2分
, 2分
又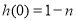 ,所以函数
,所以函数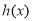 在
在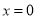 处的切线方程
处的切线方程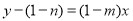 ,
,
将点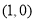 代入,得
代入,得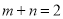 . 4分
. 4分
(2)当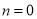 ,可得
,可得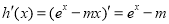 ,因为
,因为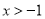 ,所以
,所以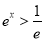 ,
,
①当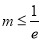 时,
时,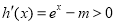 ,函数
,函数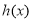 在
在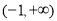 上单调递增,而
上单调递增,而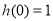 ,
,
所以只需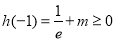 ,解得
,解得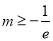 ,从而
,从而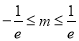 . 6分
. 6分
②当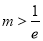 时,由
时,由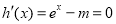 ,解得
,解得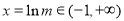 ,
,
当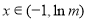 时,
时,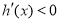 ,
,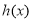 单调递减;当
单调递减;当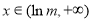 时,
时,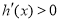 ,
,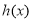 单调递增.
单调递增.
所以函数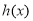 在
在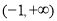 上有最小值为
上有最小值为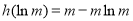 ,
,
令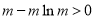 ,解得
,解得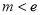 ,所以
,所以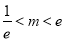 .
.
综上所述,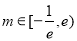 . 10分
. 10分
(3)由题意,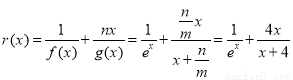 ,
,
而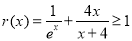 等价于
等价于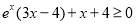 ,
,
令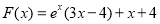 , 12分
, 12分
则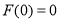 ,且
,且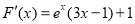 ,
,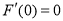 ,
,
令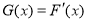 ,则
,则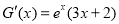 ,
,
因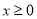 , 所以
, 所以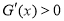 , 14分
, 14分
所以导数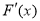 在
在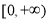 上单调递增,于是
上单调递增,于是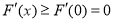 ,
,
从而函数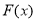 在
在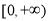 上单调递增,即
上单调递增,即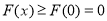 . 16分
. 16分
考点:导数几何意义,利用导数求函数单调性


科目:高中数学 来源:2014-2015学年上海市杨浦区高三上学期学业质量调研文科数学试卷(解析版) 题型:填空题
二项式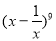 的展开式(按x的降幂排列)中的第4项是_________________.
的展开式(按x的降幂排列)中的第4项是_________________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市杨浦区高三上学期学业质量调研理科数学试卷(解析版) 题型:填空题
设△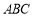 的内角
的内角 ,
,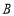 ,
,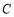 所对的边长分别为
所对的边长分别为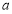 ,
, ,
,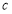 ,若
,若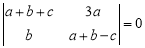 ,则角
,则角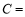 _________.
_________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省南京市、盐城市高三第一次模拟考试文科数学试卷(解析版) 题型:解答题
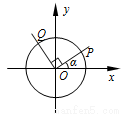
在平面直角坐标系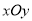 中,设锐角
中,设锐角 的始边与
的始边与 轴的非负半轴重合,终边与单位圆交于点
轴的非负半轴重合,终边与单位圆交于点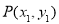 ,将射线
,将射线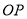 绕坐标原点
绕坐标原点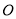 按逆时针方向旋转
按逆时针方向旋转 后与单位圆交于点
后与单位圆交于点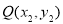 . 记
. 记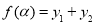 .
.
(1)求函数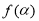 的值域;
的值域;
(2)设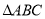 的角
的角 所对的边分别为
所对的边分别为 ,若
,若 ,且
,且 ,
,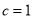 ,求
,求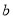 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省南京市、盐城市高三第一次模拟考试文科数学试卷(解析版) 题型:填空题
若一个圆锥的底面半径为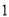 ,侧面积是底面积的
,侧面积是底面积的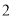 倍,则该圆锥的体积为 .
倍,则该圆锥的体积为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省南京市、盐城市高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
在平面直角坐标系 中,椭圆
中,椭圆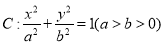 的右准线方程为
的右准线方程为 ,右顶点为
,右顶点为 ,
,
上顶点为 ,右焦点为
,右焦点为 ,斜率为
,斜率为 的直线
的直线 经过点
经过点 ,且点
,且点 到直线
到直线 的距离为
的距离为 .
.
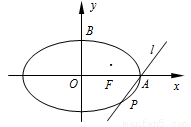
(1)求椭圆 的标准方程;
的标准方程;
(2)将直线 绕点
绕点 旋转,它与椭圆
旋转,它与椭圆 相交于另一点
相交于另一点 ,当
,当 三点共线时,试确定直线
三点共线时,试确定直线 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省江门市高三调研测试理科数学试卷(解析版) 题型:解答题
(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC.E是PC的中点,作EF⊥PB交PB于点F.

(1)求证:PA//平面EDB;
(2)求证:PF=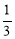 PB;
PB;
(3)求二面角C-PB-D的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com