
(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC.E是PC的中点,作EF⊥PB交PB于点F.

(1)求证:PA//平面EDB;
(2)求证:PF=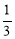 PB;
PB;
(3)求二面角C-PB-D的大小.
(1)(2)(3)
【解析】
试题分析:(1)建立适当的空间直角坐标系,设法证明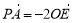 ,注意到OE
,注意到OE 平面EDB,PA
平面EDB,PA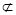 平面EDB,即可证得PA//平面EDB;
平面EDB,即可证得PA//平面EDB;
(2)设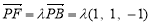 ,由
,由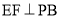 可得
可得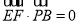 ,即可求出
,即可求出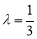 ,从而证得PF=
,从而证得PF=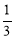 PB
PB
(3)分别求出平面PBD的一个法向量是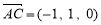 ,平面PBC的一个法向量是
,平面PBC的一个法向量是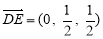 ,利用向量夹角公式可得二面角C-PB-D的大小为
,利用向量夹角公式可得二面角C-PB-D的大小为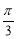
试题解析:(1)以D为原点,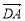 、
、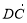 、
、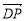 分别为
分别为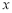 轴、
轴、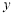 轴、
轴、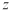 轴正方向建立空间直角坐标系,设PD=DC=1,则
轴正方向建立空间直角坐标系,设PD=DC=1,则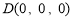 ,
,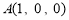 ,
, ,
,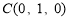 ,
,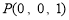 ,
,
连接AC,交BD于O,连接OE,则O是AC的中点,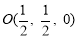
E是PC的中点,∴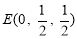 ,
,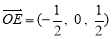
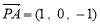 ,
,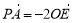 ,PA//OE
,PA//OE
OE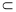 平面EDB,PA
平面EDB,PA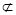 平面EDB,,∴PA//平面EDB
平面EDB,,∴PA//平面EDB
(2)设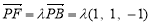 ,
,
则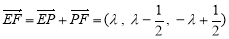
∵EF⊥PB,∴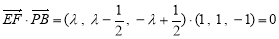
即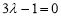 ,解得
,解得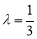 ,PF=
,PF=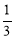 PB
PB
(3)平面PBD的一个法向量是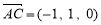
平面PBC的一个法向量是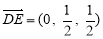
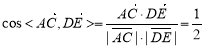
所以, ,二面角C-PB-D的大小为
,二面角C-PB-D的大小为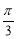
考点:线面平行判定定理,利用空间向量解决有关问题


科目:高中数学 来源:2014-2015学年江苏省南京市、盐城市高三第一次模拟考试文科数学试卷(解析版) 题型:解答题
已知函数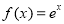 ,
,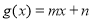 .
.
(1)设 .
.
① 若函数 在
在 处的切线过点
处的切线过点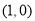 ,求
,求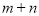 的值;
的值;
② 当 时,若函数
时,若函数 在
在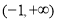 上没有零点,求
上没有零点,求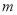 的取值范围;
的取值范围;
(2)设函数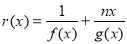 ,且
,且 ,求证:当
,求证:当 时,
时, .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省江门市高三调研测试理科数学试卷(解析版) 题型:填空题
已知数列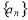 满足
满足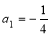 ,
,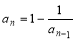 (
( ),计算并观察数列
),计算并观察数列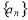 的前若干项,根据前若干项的变化规律推测,
的前若干项,根据前若干项的变化规律推测,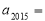 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省株洲市高三教学质量统一检测一文科数学试卷(解析版) 题型:选择题
在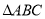 中,若角
中,若角 所对的三边
所对的三边 成等差数列,给出下列结论:
成等差数列,给出下列结论:
①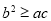 ;②
;②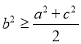 ;③
;③ ;④
;④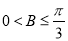 .
.
其中正确的结论是( )
A.①② B.②③ C.③④ D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com