


科目:高中数学 来源: 题型:
3+
| ||
| 2 |
3-
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:山西省康杰中学2011-2012学年高二下学期期中考试数学理科试题 题型:013
给出以下命题:
(1)若![]() ,则f(x)>0;
,则f(x)>0;
(2)![]() ;
;
(3)0比-i大
(4)两个复数互为共轭复数,当且仅当其和为实数
(5)x+yi=1+i的充要条件为x=y=1
(6)如果让实数a与ai对应,那么实数集与纯虚数集一一对应,
其中正确的命题个数是
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省高三10月联考理科数学试卷(解析版) 题型:填空题
设定义在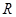 上的函数
上的函数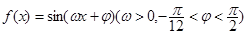 ,给出以下四个论断:
,给出以下四个论断:
①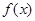 的周期为π;
②
的周期为π;
②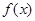 在区间(
在区间(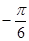 ,0)上是增函数;
,0)上是增函数;
③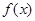 的图象关于点(
的图象关于点(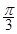 ,0)对称;④
,0)对称;④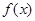 的图象关于直线
的图象关于直线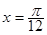 对称.
对称.
以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题(写成“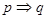 ”的形式): (其中用到的论断都用序号表示)
”的形式): (其中用到的论断都用序号表示)
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
3+
| ||
| 2 |
3-
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com