Question

（09年西城区抽样）（14分）

   如图，在底面是正方形的四棱锥P-ABCD中，平面平面ABCD，PC=PD=CD=2.

（Ⅰ）求证：；

（Ⅱ）求二面角的大小；

（Ⅲ）求点A到平面PBC的距离.

Answer 1

解析：方法一：（Ⅰ）证明：平面平面ABCD,

       又平面平面ABCD=CD，,

       平面PCD,       -----------------3分

       平面PCD,

       ；          -------------4分

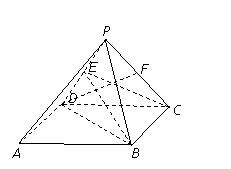
（Ⅱ）解：取PD的中点E，连接CE、BE，

为正三角形，

，

由（Ⅰ）知平面PCD,

是BE在平面PCD内的射影,

,

为二面角B-PD-C的平面角,           ---------7分

在中, , BC=2, ,

,

二面角B-PD-C的大小为；                 -------10分

（Ⅲ）解：底面ABCD为正方形，,

     平面PBC, 平面PBC,

     平面PBC,

      点A到平面PBC的距离等于点D到平面PBC的距离,       

      过D作于F,

      平面PCD，

      ,

      ,

      平面PBC, 且平面PBC=F,

      为点D到平面PBC的距离,                      ------13分

      在等边中,

      ,

      点A到平面PBC的距离等于.                  --------14分

  方法二：（Ⅰ）证明：取CD的中点为O，连接PO，

PD=PC，,

平面平面ABCD, 平面平面ABCD=CD，

       平面ABCD,       ---------------------------2分

       如图，在平面ABCD内，过O作OMCD交AB于M，

   以O为原点, OM、OC、OP分别为x、y、z轴，建立空间直角

坐标系O-xyz，

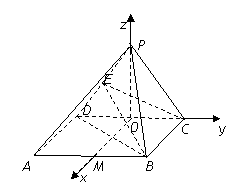
则,

       ,

；           ---------------------------4分

（Ⅱ）解：取PD的中点E，连接CE、BE，如（Ⅰ）建立空间坐标系，则，

为正三角形，

，

，

，

,

为二面角B-PD-C的平面角,                    ---------7分

         ，

         ， 

 二面角B-PD-C的大小为；                     ------------10分

（Ⅲ）解：过点A作平面PBC于F，

      为点A到平面PBC的距离, 设|AF|=h，               

       ，

       ，即,

       的面积，

三棱锥A-PBC的体积，

，

即，解得，

点A到平面PBC的距离为.                           ----------14分