
如图,
a、b是异面直线,A、BÎ a,C、DÎ b,E、F分别为线段AC和BD的中点,判断直线EF和a的位置关系,并证明你的结论.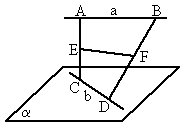
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
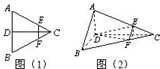 已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC边上的点,且满足
已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC边上的点,且满足| CE |
| CA |
| CF |
| CB |
| ||
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,∠OAB=
如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,∠OAB=| π | 6 |
查看答案和解析>>
科目:高中数学 来源:山东省郓城一中2012届高三上学期寒假作业数学试卷(5) 题型:013
如图所示,在直三棱柱ABC-A1B1C1中,点M、N分别在AB1、BC1上,且![]() =
=![]() =λ(0<λ<1),有以下四个结论:
=λ(0<λ<1),有以下四个结论:
①AA1⊥MN;
②AC∥MN;
③MN∥平面ABC;
④MN与AC是异面直线.其中正确的是
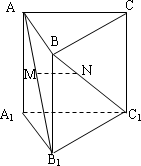
①②
①③
①④
①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年丰台区统一练习一理)(13分)
已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,
E、F分别是AC和BC边上的点,且满足![]() ,现将△ABC
,现将△ABC
沿CD翻折成直二面角A-DC-B,如图(2).
(Ⅰ) 试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(Ⅱ) 求二面角B-AC-D的大小;
(Ⅲ) 若异面直线AB与DE所成角的余弦值为![]() ,求k的值.
,求k的值.
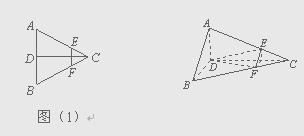
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广西省高三第二次模拟考试文科数学试卷 题型:选择题
如图,正方体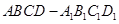 的棱长为1,线段
的棱长为1,线段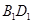 上有两个动点E、F,且
上有两个动点E、F,且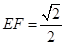 ,则下列结论中错误的是
,则下列结论中错误的是
A.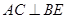 直
B.
直
B.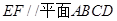
C.三棱锥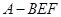 的体积为定值
D.异面直线
的体积为定值
D.异面直线 所成的角为定值
所成的角为定值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com