
【题目】有4个不同的球,4个不同的盒子,把球全部放入盒子内.
(1)共有几种放法?
(2)恰有1个空盒,有几种放法?
(3)恰有2个盒子不放球,有几种放法?
【答案】
(1)解:根据题意,4个不同的球,4个不同的盒子,
每个小球有4种放法,则4个小球共有4×4×4×4=44=256种放法
(2)解:根据题意,恰有1个空盒,即将4个小球放入3个小盒中,且三个盒子都不空;
先从4个小球中取2个放在一起,有 ![]() =6种不同的取法,
=6种不同的取法,
再把取出的两个小球与另外2个小球看作三堆,并分别放入4个盒子中的3个盒子里,有 ![]() =24种不同的放法.
=24种不同的放法.
根据分步乘法计数原理,不同的放法共有6×24=144种
(3)解:根据题意,恰有2个盒子不放球,也就是把4个不同的小球只放入2个盒子中,
有两类放法;第一类,1个盒子放3个小球,1个盒子放1个小球,
先把小球分成2组,有C43=4种分组方法,
再放到2个盒中有A42=12种放法,
则此时有4×12=48种放法;
第二类,2个盒子中各放2个小球,
先把小球分成2组,有 ![]() =3种分组方法,
=3种分组方法,
再放到2个盒中有A42=12种放法,
则此时有3×12=36种放法;
故恰有2个盒子不放球的方法共有48+36=84种
【解析】(1)根据题意,分析可得4个不同的球,每个小球有4种放法,由分步计数原理计算可得答案;(2)根据题意,恰有1个空盒,即将4个小球放入3个小盒中,且三个盒子都不空;分2步进行分析:先从4个小球中取2个放在一起,看成一个整体,再将其与另外2个小球看作三堆,并分别放入4个盒子中的3个盒子里,分别求出每一步的情况数目,由分步计数原理计算可得答案;(3)根据题意,分2种情况讨论:①、1个盒子放3个小球,1个盒子放1个小球,②2个盒子中各放2个小球,每种情况下先分组,放进其中2个盒子中,由分步计数原理可得每种情况下的放法数目,由分类计数原理计算可得答案.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +lnx,其中a为常数,e为自然对数的底数.
+lnx,其中a为常数,e为自然对数的底数.
(I)若a=1,求函数f(x)的单调区间;
(II)若函数f(x)在区间[1,2]上为单调函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在[﹣1,1]上的奇函数,f(﹣1)=﹣1,且对任意a,b∈[﹣1,1],当a≠b时,都有 ![]() ;
;
(1)解不等式f ![]() ;
;
(2)若f(x)≤m2﹣2km+1对所有x∈[﹣1,1],k∈[﹣1,1]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知( ![]() +x2)2n的展开式中各项系数的和比(3x﹣1)n的展开式中二项式系数的和大992,求(2x﹣
+x2)2n的展开式中各项系数的和比(3x﹣1)n的展开式中二项式系数的和大992,求(2x﹣ ![]() )2n的展开式中:
)2n的展开式中:
(1)第10项
(2)常数项;
(3)系数的绝对值最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、N分别是BD和AE的中点,那么①AD⊥MN;②MN∥平面CDE;③MN∥CE;④MN、CE异面.其中假命题的个数为( )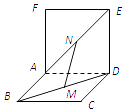
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x3﹣ax在(﹣∞,﹣1]上是单调函数,则a的取值范围是( )
A.(3,+∞)
B.[3,+∞)
C.(﹣∞,3)
D.(﹣∞,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数g(x)是奇函数f(x)(x∈R)的导函数,f(1)=0,当x>0时,xg(x)﹣f(x)<0,则使得f(x)<0成立的x的取值范围是( )
A.(﹣∞,﹣1)∪(0,1)
B.(0,1)∪(1,+∞)
C.(﹣∞,﹣1)∪(﹣1,0)
D.(﹣1,0)∪(1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com