
【题目】已知f(x)=x3+3ax2+bx+a2(a>1)在x=﹣1时的极值为0.求常数a,b的值并求f(x)的单调区间.
【答案】解:f′(x)=3x2+6ax+b,由题意知 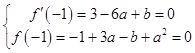 ,解得a=2,b=9…6分 所以f (x)=x3 +6x2 +9 x+4,f′(x)=3x2+12x+9
,解得a=2,b=9…6分 所以f (x)=x3 +6x2 +9 x+4,f′(x)=3x2+12x+9
由f′(x)>0可得x<﹣3或x>﹣1,所以增区间为(﹣∞,﹣3)和(﹣1,+∞)
由f′(x)<0可得﹣3<x<﹣1,所以减区间为(﹣3,﹣1)
【解析】求导函数,利用函数在x=﹣1时的极值为0,建立方程组,可求常数a,b的值;由导数的正负,可得f(x)的单调区间.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知点H(x0 , y0)在圆C:x2+y2+Dx+Ey+F=0(其中点C为圆心,D2+E2﹣4F>0)外,由点H向圆C引切线,其中一个切点为M.
求证:|HM|= ![]() ;
;
(1)已知点H(x0 , y0)在圆C:x2+y2+Dx+Ey+F=0(其中点C为圆心,D2+E2﹣4F>0)外,由点H向圆C引切线,其中一个切点为M.
求证:|HM|= ![]() ;
;
(2)如图,P是直线x=4上一动点,以P为圆心的圆P经定点B(1,0),直线l是圆P在点B处的切线,过A(﹣1,0)作圆P的两条切线分别与l交于E,F两点.
求证:|EA|+|EB|为定值.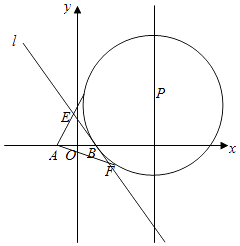
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和记为Sn , a1=t,an+1=2Sn+1(n∈N*).
(1)当t为何值时,数列{an}为等比数列?
(2)在(1)的条件下,若等差数列{bn}的前n项和Tn有最大值,且T3=15,又a1+b1 , a2+b2 , a3+b3成等比数列,求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD的平行四边形,∠ADC=60°, ![]() ,PA⊥面ABCD,E为PD的中点.
,PA⊥面ABCD,E为PD的中点.
(Ⅰ)求证:AB⊥PC
(Ⅱ)若PA=AB= ![]() ,求三棱锥P﹣AEC的体积.
,求三棱锥P﹣AEC的体积.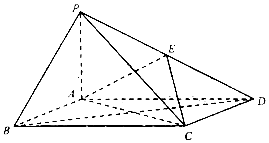
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣(a﹣1)x2+b2x,其中a∈{1,2,3,4},b∈{1,2,3},则函数f(x)在R上是增函数的概率为( )
x3﹣(a﹣1)x2+b2x,其中a∈{1,2,3,4},b∈{1,2,3},则函数f(x)在R上是增函数的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足:f′(x)>1﹣f(x),f(0)=6,f′(x)是f(x)的导函数,则不等式 ![]() (其中e为自然对数的底数)的解集为( )
(其中e为自然对数的底数)的解集为( )
A.(0,+∞)
B.(﹣∞,0)∪(3,+∞)
C.(﹣∞,0)∪(1,+∞)
D.(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4个不同的球,4个不同的盒子,把球全部放入盒子内.
(1)共有几种放法?
(2)恰有1个空盒,有几种放法?
(3)恰有2个盒子不放球,有几种放法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com