
分析 根据题意,分5种情况讨论:①、四位同学都选甲题目,则其中2人答对、2人答错,②、四位同学都选乙题目,则其中2人答对、2人答错,③、四位同学中2人选甲,其中1人答对、1人答错;剩下2人选乙,其中1人答对、1人答错,④、四位同学中3人选甲,且回答正确;剩下1人选乙,且回答错误,⑤、四位同学中3人选甲,且回答错误;剩下1人选乙,且回答正确,分别求出每一种情况下的不同的得分情况数目,由分类计数原理计算可得答案.
解答 解:根据题意,分5种情况讨论:
①、四位同学都选甲题目,则其中2人答对、2人答错,有C42=6种情况;
②、四位同学都选乙题目,则其中2人答对、2人答错,有C42=6种情况;
③、四位同学中2人选甲,其中1人答对、1人答错;剩下2人选乙,其中1人答对、1人答错,有C42×A22×A22=24种情况,
④、四位同学中3人选甲,且回答正确;剩下1人选乙,且回答错误,有C43=4种情况,
⑤、四位同学中3人选甲,且回答错误;剩下1人选乙,且回答正确,有C43=4种情况,
则一共有6+6+24+4+4=44种情况;
故答案为:44.
点评 本题考查排列、组合的实际运用,关键是依据题意,进行分析讨论.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}-\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}-\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}+\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}+\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
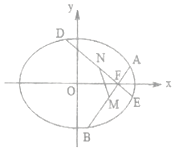 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{2}}}{2}$,且过点$(\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2})$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{2}}}{2}$,且过点$(\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2})$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 函数 f(x)=Acos(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R),其部分图象如图所示.
函数 f(x)=Acos(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R),其部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com