a.b.c是三条直线.α.β是两个平面.b?α.c?α．则下列命题不成立的是( )A．若α∥β.c⊥α.则c⊥βB．“若b⊥β.则α⊥β 的逆命题C．若a是c在α的射影.a⊥b.则b⊥cD．“若b∥c.则c∥α 的逆否命题题目和参考答案——青夏教育精英家教网—

4．a、b、c是三条直线，α、β是两个平面，b?α，c?α．则下列命题不成立的是（　　）

	A．	若α∥β，c⊥α，则c⊥β		B．	“若b⊥β，则α⊥β”的逆命题
	C．	若a是c在α的射影，a⊥b，则b⊥c		D．	“若b∥c，则c∥α”的逆否命题

分析用空间中线面的位置关系对四个选项逐一判断得出正确选项，A选项用线面垂直证明；B选项用线面垂直证明；C选项用线线垂直的条件来证；D选项用线线平行的条件来证．

解答解：A选项中命题正确，因为一条直线垂直于两个平行平面中的一个，也垂直于另一个；
B选项不正确，因为两面垂直与线面垂直没有关系；
C选项中命题成立
D选项中，这个命题正确，则它的逆否命题正确，
故选B．

点评本题考查四种命题之间的关系，这种题目需要挨个判断说法是否正确，注意在判断时不要忽略几个特殊情况．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

8．已知函数$f（x）=\frac{{5-x+{4^x}}}{2}-\frac{{|{5-x-{4^x}}|}}{2}$，则f（x）的单调增区间为（-∞，1]，$f（x）＞\sqrt{5}$的解集为（1，5-$\sqrt{5}$）∪（log₄$\sqrt{5}$，1]．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

9．当用反证法证明“已知x＞y，证明：x³＞y³”时，假设的内容应是（　　）

A．

x³≤y³

B．

x³＜y³

C．

x³＞y³

D．

x³≥y³

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．已知函数f（x）=xlnx-k（x-1）
（1）求f（x）的单调区间；并证明lnx+$\frac{e}{x}$≥2（e为自然对数的底数）恒成立；
（2）若函数f（x）的一个零点为x₁（x₁＞1），f'（x）的一个零点为x₀，是否存在实数k，使$\frac{x_1}{x_0}$=k，若存在，求出所有满足条件的k的值；若不存在，说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

13．已知p：x（x-2）≥0，q：|x-2|＜1，其中x是实数．
（1）若命题“￢p”为真，求x的取值范围；
（2）若命题p，命题q都为真，求x的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．已知平面直角坐标系中两定点为A（2，3），B（5，3），若动点M满足|AM|=2|BM|．
（1）求动点M的轨迹方程；
（2）若直线l：y=x-5与M的轨迹交于C，D两点，求CD的长度．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

16．已知以下列联表，且已知P（K²≥6.635）≈0.010，根据此列联表求得随机变量K²的观测值k≈16.373＞6.635，那么以下说法正确的是（　　）

	患心脏病	患其它病	总计
秃顶	214	175	389
不秃顶	451	597	1048
总计	665	772	1437

	A．	秃顶与患心脏病一定有关系
	B．	在犯错误的概率不超过0.010的前提下，认为秃顶与患心脏病有关系
	C．	我们有1%的把握认为秃顶与患心脏病有关系
	D．	在犯错误的概率不超过0.010的前提下，认为秃顶与患心脏病没有关系

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

13．

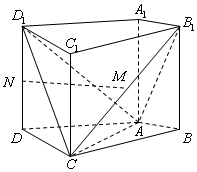如图，在四棱柱ABCD-A₁B₁C₁D₁中，侧棱A₁A⊥底面ABCD，AB⊥AC，AB=3，AC=AA₁=6，AD=CD=5，且点M和N分别为B₁C和D₁D的中点．
（1）求证：MN∥平面ABCD；
（2）求二面角D₁-AC-B₁的正切值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

14．已知函数$f（{x^2}-1）={log_m}\frac{{2-{x^2}}}{x^2}（m＞1）$
（1）求f（x）的解析式，并判断f（x）的奇偶性；
（2）比较$f（ln\sqrt{e}）$与$f（\frac{1}{3}）$的大小，并写出必要的理由．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学