
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D= ![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.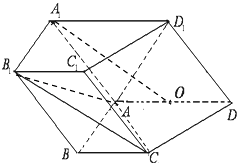
(Ⅰ)求证:A1O∥平面AB1C;
(Ⅱ)求锐二面角A﹣C1D1﹣C的余弦值.
【答案】(Ⅰ)证明:如图,连接CO,AC,
则四边形ABCO为正方形,
∴OC=AB=A1B1,且OC∥AB∥A1B1
∴四边形A1B1CO为平行四边形,
∴A1O∥B1C,
又∵A1O平面AB1C,B1C平面AB1C,
∴A1O∥平面AB1C.…
(Ⅱ)∵D1A=D1D,O为AD的中点,
∴D1O⊥AD,又侧面ADD1A1⊥底面ABCD,
∴D1O⊥底面ABCD,…
以O为原点,OC,OD,OD1所在直线分别为x轴,y轴,Z轴,
建立如图所示的坐标系,
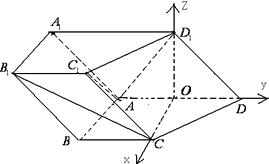
由题意得:C(1,0,0),D(0,1,0),
D1(0,0,1),A(0,﹣1,0),…
∴ ![]() ,
, ![]() =(0,﹣1,1),
=(0,﹣1,1),
![]() =(0,﹣1,﹣1),
=(0,﹣1,﹣1), ![]() =(1,﹣1,0),
=(1,﹣1,0),
设 ![]() 为平面CDD1C1的一个法向量,
为平面CDD1C1的一个法向量,
则 ![]() ,∴
,∴ ![]() ,
,
令Z=1,则y=1,x=1,∴ ![]() ,…
,…
设 ![]() 为平面AC1D1的一个法向量,
为平面AC1D1的一个法向量,
则 ![]() ,∴
,∴ ![]() ,令Z1=1,
,令Z1=1,
则y1=﹣1,x1=﹣1,∴ ![]() ,
,
∴ ![]() ,
,
∴所求锐二面角A﹣C1D1﹣C的余弦值为 ![]() .…
.…
【解析】(1)连接CO,AC易证![]() 为平行四边形,由此可证
为平行四边形,由此可证![]() ∥平面
∥平面![]() ;(2)以O为坐标原点,OC,OD,
;(2)以O为坐标原点,OC,OD,![]() 为x,y,z轴建立空间直角坐标系,利用法向量求出锐二面角。
为x,y,z轴建立空间直角坐标系,利用法向量求出锐二面角。
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中,椭圆C1: ![]() 的左、右焦点分别为F1 , F2 , 其中F2也是抛物线C2:y2=4x的焦点,点P为C1与C2在第一象限的交点,且
的左、右焦点分别为F1 , F2 , 其中F2也是抛物线C2:y2=4x的焦点,点P为C1与C2在第一象限的交点,且 ![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过F2且与坐标轴不垂直的直线交椭圆于M、N两点,若线段OF2上存在定点T(t,0)使得以TM、TN为邻边的四边形是菱形,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块以点O为圆心,半径为2百米的圆形草坪,草坪内距离O点 ![]() 百米的D点有一用于灌溉的水笼头,现准备过点D修一条笔直小路交草坪圆周于A,B两点,为了方便居民散步,同时修建小路OA,OB,其中小路的宽度忽略不计.
百米的D点有一用于灌溉的水笼头,现准备过点D修一条笔直小路交草坪圆周于A,B两点,为了方便居民散步,同时修建小路OA,OB,其中小路的宽度忽略不计.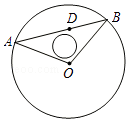
(1)若要使修建的小路的费用最省,试求小路的最短长度;
(2)若要在△ABO区域内(含边界)规划出一块圆形的场地用于老年人跳广场舞,试求这块圆形广场的最大面积.(结果保留根号和π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公比为q(q≠1)的等比数列a1 , a2 , a3 , a4 , 若删去其中的某一项后,剩余的三项(不改变原有顺序)成等差数列,则所有满足条件的q的取值的代数和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx+(1﹣x)ln(1﹣x),x∈(0,1).
(1)求f(x)的最小值;
(2)若a+b+c=1,a,b,c∈(0,1).求证:alna+blnb+clnc≥(a﹣2)ln2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() (ω>0)的图象与x轴正半轴交点的横坐标构成一个公差为
(ω>0)的图象与x轴正半轴交点的横坐标构成一个公差为 ![]() 的等差数列,若要得到函数g(x)=Asinωx的图象,只要将f(x)的图象( )个单位.
的等差数列,若要得到函数g(x)=Asinωx的图象,只要将f(x)的图象( )个单位.
A.向左平移 ![]()
B.向右平移 ![]()
C.向左平移 ![]()
D.向右平移 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科技公司生产一种手机加密芯片,其质量按测试指标划分为:指标大于或等于70为合格品,小于70为次品.现随机抽取这种芯片共120件进行检测,检测结果统计如表:
测试指标 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
芯片数量(件) | 8 | 22 | 45 | 37 | 8 |
已知生产一件芯片,若是合格品可盈利400元,若是次品则亏损50元.
(Ⅰ)试估计生产一件芯片为合格品的概率;并求生产3件芯片所获得的利润不少于700元的概率.
(Ⅱ)记ξ为生产4件芯片所得的总利润,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上,点A、C为射线PM上的两点,点B、D为射线PN上的两点,则有 ![]() (其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有
(其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有 ![]() =(其中VP﹣ABE、VP﹣CDF分别为四面体P﹣ABE、P﹣CDF的体积).
=(其中VP﹣ABE、VP﹣CDF分别为四面体P﹣ABE、P﹣CDF的体积).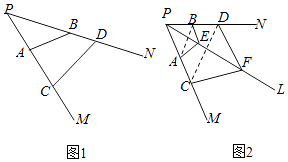
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0),F为其焦点,过点(4,0)作垂直于x轴的直线交抛物线于A,B两点,△ABF的周长为18.
(1)求抛物线的方程;
(2)过抛物线上的定点 ![]() 作两条关于直线y=p对称的直线分别交抛物线于C,D两点,连接CD,判断直线CD的斜率是否为定值?并证明你的结论.
作两条关于直线y=p对称的直线分别交抛物线于C,D两点,连接CD,判断直线CD的斜率是否为定值?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com