
【题目】公比为q(q≠1)的等比数列a1 , a2 , a3 , a4 , 若删去其中的某一项后,剩余的三项(不改变原有顺序)成等差数列,则所有满足条件的q的取值的代数和为 .
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知公差不为0的等差数列{an}中,a1 , a3 , a7成等比数列,且a2n=2an﹣1,等比数列{bn}满足bn+bn+1= ![]() .
.
(1)求数列{an},{bn}的通项公式;
(2)令cn=anbn , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过点P(0,1)且互相垂直的两条直线分别与
圆O:x2+y2=4交于点A,B,与圆M:(x﹣2)2+(y﹣1)2=1交于点C,D.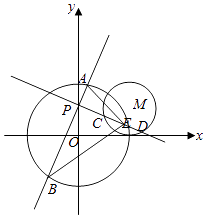
(1)若 ![]() ,求CD的长;
,求CD的长;
(2)若CD中点为E,求△ABE面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线l的普通方程为x﹣y﹣2=0,曲线C的参数方程为 ![]() (θ为参数),设直线l与曲线C交于A,B两点.若点P在曲线C上运动,当△PAB的面积最大时,求点P的坐标及△PAB的最大面积.
(θ为参数),设直线l与曲线C交于A,B两点.若点P在曲线C上运动,当△PAB的面积最大时,求点P的坐标及△PAB的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张于年初支出50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元.小张在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x年年底出售,其销售收入为25﹣x万元(国家规定大货车的报废年限为10年).
(1)大货车运输到第几年年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小张获得的年平均利润最大?(利润=累计收入+销售收入﹣总支出)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}是各项均为正数的等比数列,其前n项和为Sn , 且a1a5=64,S5﹣S3=48.
(1)求数列{an}的通项公式;
(2)设有正整数m,l(5<m<l),使得am , 5a5 , al成等差数列,求m,l的值;
(3)设k,m,l∈N*,k<m<1,对于给定的k,求三个数 5ak , am , al经适当排序后能构成等差数列的充要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D= ![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.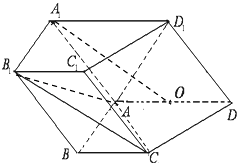
(Ⅰ)求证:A1O∥平面AB1C;
(Ⅱ)求锐二面角A﹣C1D1﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间[﹣3,3]上的单调函数f(x)满足:对任意的x∈[﹣3,3],都有f(f(x)﹣2x)=6,则在[﹣3,3]上随机取一个实数x,使得f(x)的值不小于4的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是( )
(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸;③台体的体积公式V= ![]() )
)
A.2寸
B.3寸
C.4寸
D.5寸
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com