
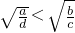 ;②已知a、b、m都是正数,并且a<b,则
;②已知a、b、m都是正数,并且a<b,则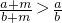 ;③若a、b∈R,则a2+b2+5≥2(2a-b);④函数f(x)=2-3x-
;③若a、b∈R,则a2+b2+5≥2(2a-b);④函数f(x)=2-3x- 的最大值是2-4
的最大值是2-4 .其中正确命题的序号是________把你认为正确命题的序号都填上)
.其中正确命题的序号是________把你认为正确命题的序号都填上)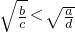 ,故①不正确;对于②,利用作差比较的方法,得到
,故①不正确;对于②,利用作差比较的方法,得到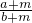 与
与 差的式子,再讨论这个差的各个因式的正负,得到
差的式子,再讨论这个差的各个因式的正负,得到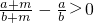 ,从而得到②正确;对于③,将a2+b2+5与2(2a-b)作差,再将这个差配方得到(a-2)2+(b-1)2,利用平方非负的性质可得到③正确;对于④,首先证明|3x+
,从而得到②正确;对于③,将a2+b2+5与2(2a-b)作差,再将这个差配方得到(a-2)2+(b-1)2,利用平方非负的性质可得到③正确;对于④,首先证明|3x+ |≥4
|≥4 ,从而得出3x+
,从而得出3x+ ≤-4
≤-4 或3x+
或3x+ ≥4
≥4 ,所以函数f(x)=2-3x-
,所以函数f(x)=2-3x- 的值域为(-∞,2-4
的值域为(-∞,2-4 ]∪[2+4
]∪[2+4 ,+∞),函数没有最大值,故④不正确.由此得到正确答案.
,+∞),函数没有最大值,故④不正确.由此得到正确答案.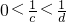 且0<b<a
且0<b<a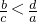 ?
?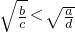 ,故①不正确;
,故①不正确;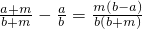
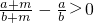 ,故
,故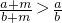 ,②正确;
,②正确; =2-(3x+
=2-(3x+ ),
), |≥2
|≥2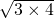 =4
=4 ,得3x+
,得3x+ ≤-4
≤-4 或3x+
或3x+ ≥4
≥4 ,
, 的值域为(-∞,2-4
的值域为(-∞,2-4 ]∪[2+4
]∪[2+4 ,+∞),
,+∞),

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| y-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 12 |
| π |
| 12 |
| x |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2x-1 |
| (1+2x)2 |
| x•2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com