试题分析:(1)由对数函数的真数大于零求解.
(2)当函数在定义域上单调时,则不存在,当函数在定义域上不单调时,则存在,所以要证明函数是否单调,可用定义法,也可用导数法研究.
(3)由“f(x)在(1,+∞)上恒取正值”则需函数的最小值非负即可,由(2)可知是增函数,所以只要f(1)≥0即可.
解 :(1)由a
x-b
x>0,
得(
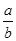
)
x>1,且a>1>b>0,得
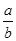
>1,
所以x>0,即f(x)的定义域为(0,+∞).
(2)任取x
1>x
2>0,a>1>b>0,则ax
1>ax
2>0,bx
1<bx
2,所以ax
1-bx
1>ax
2-bx
2>0,
即lg(a
x1-b
x1)>lg(a
x2-b
x2). 故f(x
1)>f(x
2).
所以f(x)在(0,+∞)上为增函数.
假设函数y=f(x)的图象上存在不同的两点A(x
1,y
1)、B(x
2,y
2),使直线平行于x轴, 则x
1≠x
2,y
1=y
2,这与f(x)是增函数矛盾.
故函数y=f(x)的图象上不存在不同的两点使过两点的直线平行于x轴.
(3)因为f(x)是增函数,
所以当x∈(1,+∞)时,f(x)>f(1). 这样只需f(1)=lg(a-b)≥0,
即当a≥b+1时, f(x)在(1,+∞)上恒取正值.
点评:解决该试题的关键是利用导数的几何意义来表示切线的斜率,同时能利用对数的真数大于零得到定义域进而研究其性质。

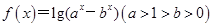 .
.  的定义域;
的定义域; 的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
的图象上是否存在不同的两点,使得过这两点的直线平行于x轴; 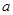 ,b满足什么条件时,
,b满足什么条件时,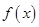 在
在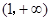 上恒取正值.
上恒取正值.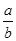 )x>1,且a>1>b>0,得
)x>1,且a>1>b>0,得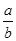 >1,
>1,

 阅读快车系列答案
阅读快车系列答案