
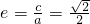 ,并确定这样的
,并确定这样的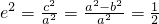 的个数.
的个数. <e,所以f(x)在[-2,+∞)上的最小值为f(-2),
<e,所以f(x)在[-2,+∞)上的最小值为f(-2), ,
,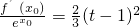 ,即为
,即为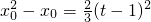 ,
,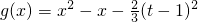 ,
,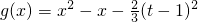 =0在(-2,t)上有解,
=0在(-2,t)上有解,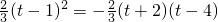 ,
,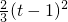 =
=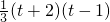 ,
,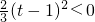 ,
,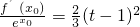 ,
, <e,所以f(x)在[-2,+∞)上的最小值为f(-2),由此能够证明n>m.
<e,所以f(x)在[-2,+∞)上的最小值为f(-2),由此能够证明n>m. ,所以
,所以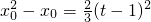 ,令
,令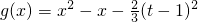 ,问题转化为证明方程
,问题转化为证明方程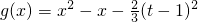 =0在(-2,t)上有解.由此能够证明对于任意的t>-2,总存在x0∈(-2,t),满足
=0在(-2,t)上有解.由此能够证明对于任意的t>-2,总存在x0∈(-2,t),满足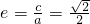 ,并能确定这样的
,并能确定这样的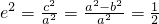 的个数.
的个数.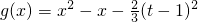 =0在(-2,t)上有解,是高考的重点.解题时要认真审题,仔细解答.
=0在(-2,t)上有解,是高考的重点.解题时要认真审题,仔细解答. 

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| m |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com