
A. | B. | C. | D. |
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源:不详 题型:解答题
 三个社区参加社会实践,要求每个社区至少有一名同学.
三个社区参加社会实践,要求每个社区至少有一名同学. 社区的概率;
社区的概率; 为四名同学中到
为四名同学中到 社区的人数,求
社区的人数,求 的分布列和
的分布列和 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、
、 两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品. 表示其中合格品的个数,求
表示其中合格品的个数,求 的分布列及数学期望
的分布列及数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,
, ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立. π(x∈R)是偶函数”为事件D,求事件D发生的概率.
π(x∈R)是偶函数”为事件D,求事件D发生的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,取到黑球或黄球的概率是
,取到黑球或黄球的概率是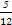 ,取到黄球或绿球的概率也是
,取到黄球或绿球的概率也是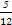 ,则取到黑球、黄球、绿球的概率分别是 .
,则取到黑球、黄球、绿球的概率分别是 .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 |2的所有取值之和;
|2的所有取值之和; |2取得最大值”的概率.
|2取得最大值”的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ( )
( )A.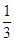 | B.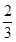 | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. ; ; | B.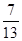 ; ; | C.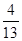 ; ; | D. . . |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com