
 三个社区参加社会实践,要求每个社区至少有一名同学.
三个社区参加社会实践,要求每个社区至少有一名同学. 社区的概率;
社区的概率; 为四名同学中到
为四名同学中到 社区的人数,求
社区的人数,求 的分布列和
的分布列和 的值.
的值. 社区的概率是
社区的概率是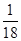 .
.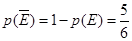 .
. 可能取的值为1,2.
可能取的值为1,2. 的分布列是:
的分布列是: |  | 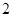 |
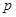 | 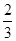 | 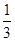 |
 .
. .
.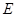 ,那么
,那么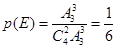 ,根据对立事件的概率公式,甲、乙两人不在同一社区的概率是
,根据对立事件的概率公式,甲、乙两人不在同一社区的概率是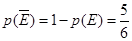 ;
; 可能取的值为1,2.事件“
可能取的值为1,2.事件“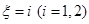 ”是指有
”是指有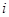 个同学到
个同学到 社区,由古典概型概率的计算即可得到分布列,进一步计算得数学期望.
社区,由古典概型概率的计算即可得到分布列,进一步计算得数学期望. 社区为事件
社区为事件 ,那么
,那么 ,
, 社区的概率是
社区的概率是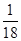 . 2分
. 2分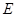 ,那么
,那么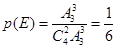 , 4分
, 4分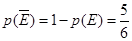 . 6分
. 6分 可能取的值为1,2.事件“
可能取的值为1,2.事件“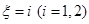 ”是指有
”是指有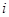 个同学到
个同学到 社区,
社区, . 8分
. 8分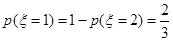 , 10分
, 10分 |  | 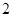 |
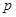 | 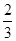 | 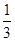 |
 的分布列是:
的分布列是: . 12分
. 12分

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源:不详 题型:解答题
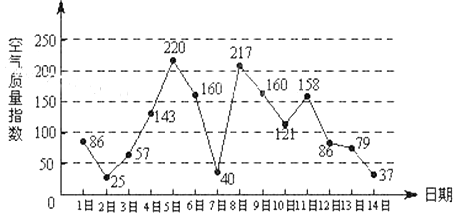
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 健康指数 | 2 | 1 | 0 | -1 |
| 60岁至79岁的人数 | 250 | 260 | 65 | 25 |
| 80岁及以上的人数 | 20 | 45 | 20 | 15 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
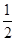 ,P(B)=
,P(B)= ,则出现奇数点或2点的概率为________.
,则出现奇数点或2点的概率为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com