
钝角△ABC的三内角A、B、C所对的边分别为a、b、c,sinC=  ,
,
(c-b)sin2A+bsin2B=csin2C,求角A、B、C.
解:由(c-b)sin2A+bsin2B=csin2C,
得(c-b)a2+b3=c3,
所以(c-b)a2+(b-c)(b2+bc+c2)=0,
即(c-b)(b2+bc+c2-a2)=0,
所以b=c或b2+bc+c2-a2=0,
当b=c时,有B=C,所以C为锐角,
又sinC= 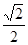 ,所以B=C=45°,
,所以B=C=45°,
所以A=90°,这与△ABC为钝角三角形矛盾
当b2+bc+c2-a2=0时,b2+c2-a2=-bc,
所以cosA=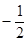
所以A=120°,
又sinC= 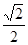 且C为锐角,所以C=45°,
且C为锐角,所以C=45°,
所以B=180°-A-C=15°,
综上可知,A=120°,B=15°,C=45°.
【解析】略


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)若方程组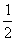 有实数解,求k的值.
有实数解,求k的值.
(2)对于(1)中k值,若sinC=![]() ,且有关系式(c-b)sin
,且有关系式(c-b)sin
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com