练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，正方形ACC1A1与等腰直角△ACB互相垂直，∠ACB＝90°，EF分别是ABBC的中点，G是AA1上的点．

    (Ⅰ)若，试确定点G的位置；

    (Ⅱ)在满足条件(1)的情况下，试求cos＜，＞的值．

    答案：空间向量与立体几何的运用
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，在棱长为1的正方体AC1中，E、F分别为A1D1和A1B1的中点．
    （1）求异面直线AF和BE所成的角的余弦值：
    （2）求平面ACC1与平面BFC1所成的锐二面角：
    （3）若点P在正方形ABCD内部或其边界上，且EP∥平面BFC1，求EP的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

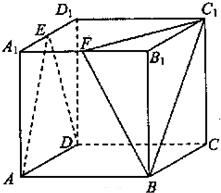    如图，在棱长为1的正方体AC1中，E、F分别为A1D1和A1B1的中点．
    （1）求异面直线AF和BE所成的角的余弦值：
    （2）求平面ACC1与平面BFC1所成的锐二面角：
    （3）若点P在正方形ABCD内部或其边界上，且EP∥平面BFC1，求EP的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年浙江省宁波市万里国际学校高二（下）期末数学试卷（理科）（解析版） 题型：解答题

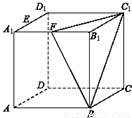    如图，在棱长为1的正方体AC1中，E、F分别为A1D1和A1B1的中点．
    （1）求异面直线AF和BE所成的角的余弦值：
    （2）求平面ACC1与平面BFC1所成的锐二面角：
    （3）若点P在正方形ABCD内部或其边界上，且EP∥平面BFC1，求EP的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：《立体几何》2013年广东省广州大学附中高考数学二轮检测（解析版） 题型：解答题

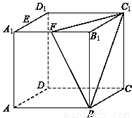    如图，在棱长为1的正方体AC1中，E、F分别为A1D1和A1B1的中点．
    （1）求异面直线AF和BE所成的角的余弦值：
    （2）求平面ACC1与平面BFC1所成的锐二面角：
    （3）若点P在正方形ABCD内部或其边界上，且EP∥平面BFC1，求EP的取值范围．

    查看答案和解析>>

    同步练习册答案