
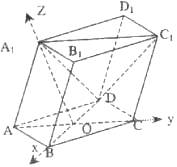
(08年长沙市模拟理)(12分) 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,![]() ,平面
,平面![]() 平面
平面![]() 。
。
(1)证明:![]() ;
;
(2)求二面角D-A1A-C的平面角的余弦值;
(3)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由。
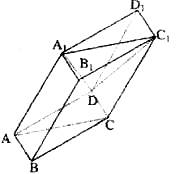
解析:连接BD交AC于O,则![]() ,连接A1O在
,连接A1O在![]() 中,AA1=2,AO=1,
中,AA1=2,AO=1,
![]()
![]()
![]()
![]() ,由于平面
,由于平面![]() 平面ABCD,
平面ABCD,
所以![]() 底面ABCD
底面ABCD
∴以OB、OC、OA1所在直线为x轴、y轴、z轴建立如图所示空间直角坐标系,则A(0,-1,0),B(![]() ,0,0),C(0,1,0),D(-
,0,0),C(0,1,0),D(-![]() ,0,0),A1(0,0,
,0,0),A1(0,0, ![]() ) 2分
) 2分
(1)由于![]()
由![]()
![]() 4分
4分
(2)由于![]() 平面
平面![]() 平面AA1C1C的法向量
平面AA1C1C的法向量![]() ,设
,设![]() 平面AA1D,则
平面AA1D,则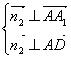 设
设![]() 6分
6分
得到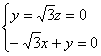 取
取![]() 6分
6分
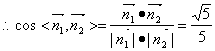
所以二面角D-A1A-C的平面角的余弦值是![]() 8分
8分
(3)假设在直线CC1上存在点P,使BP//平面DA1C1
设![]() 则
则![]()
得![]() 9分
9分
设![]() 平面DA1C1,则
平面DA1C1,则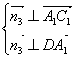 ,设
,设![]()
得到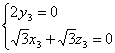 不妨取
不妨取![]() 10分
10分
又因为![]() 平面DA1C1,则
平面DA1C1,则![]() 即
即![]() 得
得![]()
即点P在C1C的延长线上且使C1C=CP 12分
法二:过A1作![]() 于点O,由于平面
于点O,由于平面![]() 平面ABCD,由面面垂直的性质定理知,
平面ABCD,由面面垂直的性质定理知,![]() 平面ABCD,又底面为菱形,所以
平面ABCD,又底面为菱形,所以![]()
 4分
4分
(2)在![]() 中,
中,![]() 。
。
![]()
所以O是AC的中点,由于底面ABCD为菱形,所以O也是BD中点
由(1)可知![]() 平面AA1C
平面AA1C
过O作![]() 于E点,连接OE,则
于E点,连接OE,则![]()
则![]() 为二面角D-AA1-C的平面角 6分
为二面角D-AA1-C的平面角 6分
在菱形ABCD中,![]()
![]()
![]()
在![]() 中,
中,![]()
![]() 8分
8分
(3)以下同解法1。


科目:高中数学 来源: 题型:
(08年长沙市模拟理)(13分)已知数列{an}的前n项和Sn满足Sn=-1,Sn+1+2Sn=-1(![]() ),数列{bn}的通项公式为
),数列{bn}的通项公式为![]() 。
。
(1)求数列![]() 的通项公式;
的通项公式;
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年长沙市模拟理)(13分) 已知椭圆C的焦点在x轴上,它的一个顶点恰好是抛物线![]() 的焦点,离心率
的焦点,离心率![]() 。
。
(1)求椭圆的标准方程;
(2)过椭圆C的右焦点作直线l交椭圆C于A、B两点,交y轴于M,若![]() 为定值吗?证明你的结论。
为定值吗?证明你的结论。
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年长沙市模拟理)(12分)现有甲、乙两个项目,对甲项目每投资十万元,一年后利润是1.2万元,1.18万元,1.17万元的概率分别为![]() ;已知乙项目的利润与产品价格调整有关,在每次调整中价格下降的概率为P(0<P<1),记乙项目产品价格在一年内进行2次独立调整,设乙项目产品价格在一年内的下降次数为
;已知乙项目的利润与产品价格调整有关,在每次调整中价格下降的概率为P(0<P<1),记乙项目产品价格在一年内进行2次独立调整,设乙项目产品价格在一年内的下降次数为![]() ,对乙项目再投资十万元,
,对乙项目再投资十万元,![]() 以0,1,2时产品价格在一年后的利润是1.3万元,1.25万元,0.2万元。随机变量
以0,1,2时产品价格在一年后的利润是1.3万元,1.25万元,0.2万元。随机变量![]() 1,
1,![]() 2分别表示甲、乙两项目各投资十万元一年后的利润。
2分别表示甲、乙两项目各投资十万元一年后的利润。
(1)求![]() 1,
1,![]() 2的概率分布列和数学期望E
2的概率分布列和数学期望E![]() 1,E
1,E![]() 2;
2;
(2)当E![]() 1,E
1,E![]() 2时,求P的范围。
2时,求P的范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com