练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    圆C过点P(1,2)和Q(-2,3),且圆C在两坐标轴上截得的弦长相等,求圆C的方程.

    x2+y2+2x-2y-3=0或x2+y2+4x+4y-17=0.


    解析:

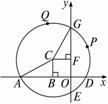
    如图所示,由于圆C在两坐标轴上的弦长相等,即|AD|=EG|,所以它们的一半也相等,即|AB|=|GF|.

    又|AC|=|GC|,

    ∴Rt△ABC≌Rt△GFC.

    ∴|BC|=|FC|.

    设C(a,b),则|a|=|b|.①

    又圆C过点P(1,2)和Q(-2,3),

    ∴圆心在PQ的垂直平分线上,

    即,即y=3x+4.∴b=3a+4.②

    由①知a=±b,代入②

    ∴或5.

    故所求的圆的方程为(x+1)2+(y-1)2=5或(x+2)2+(y+2)2=25,

    即x2+y2+2x-2y-3=0或x2+y2+4x+4y-17=0.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知圆C过点P（1，1），且与圆M：（x+2）2+（y+2）2=r2（r＞0）关于x+y+2=0对称．
    （Ⅰ）求圆C的方程；
    （Ⅱ）过点（
    		2
    ，2）作圆C的切线，求切线的方程；
    （Ⅲ）过点P作两条相异直线分别与圆C相交A，B两点，设直线PA和直线PB的斜率分别为k，-k，O为坐标原点，试判断直线OP和直线AB是否平行？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点O为坐标原点，圆C过点（1，1）和点（-2，4），且圆心在y轴上．
    （1）求圆C的标准方程；
    （2）如果过点P（1，0）的直线l与圆C有公共点，求直线l的斜率k的取值范围；
    （3）如果过点P（1，0）的直线l与圆C交于A、B两点，且|AB|=2
    		3
    ，试求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源：江苏省扬州中学2011－2012学年高二上学期期中考试数学试题 题型：044

    已知圆C过点P(1，1)，且与圆(x＋3)2＋(y＋3)2＝r2(r＞0)关于直线x＋y＋3＝0对称．

    (1)求圆C的方程；

    (2)过点P作两条直线分别与圆C相交于点A、B，且直线PA和直线PB的倾斜角互补，O为坐标原点，判断直线OP与AB是否平行，并请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2013届江苏灌南高级中学高三上期中考试文科数学试卷（带解析） 题型：解答题

    （本小题满分16分）
    已知圆C过点P(1，1)，且与圆M：＋＝(r＞0)关于直线x＋y＋2＝0对称．
    （1）求圆C的方程；
    （2）直线l过点Q(1，0.5),截圆C所得的弦长为2,求直线l的方程；
    （3）过点P作两条相异直线分别与圆C相交于A，B，且直线PA和直线PB的倾斜角互补，O为坐标原点，试判断直线OP和AB是否平行？请说明理由．

    查看答案和解析>>

    同步练习册答案