
 ,
, ),a•b=
),a•b= ,且
,且 <x<
<x< ,则cos(x+
,则cos(x+ )的值为
)的值为



 、
、 的坐标,得
的坐标,得 •
• =
= (cosx+sinx)=
(cosx+sinx)= ,解出cosx+sinx=
,解出cosx+sinx= .由同角三角函数的关系,得(cosx-sinx)2=
.由同角三角函数的关系,得(cosx-sinx)2=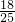 ,结合
,结合 <x<
<x< 知cosx-sinx为负数,得cosx-sinx=-
知cosx-sinx为负数,得cosx-sinx=-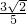 ,最后根据两角和的余弦公式,可得cos(x+
,最后根据两角和的余弦公式,可得cos(x+ )的值.
)的值. =(cosx,sinx),
=(cosx,sinx), =(
=( ,
, ),
), •
• =
= cosx+
cosx+ sinx=
sinx= ,得cosx+sinx=
,得cosx+sinx=
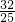 =
=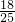
 <x<
<x< ,
, =-
=-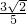
 )=cosxcos
)=cosxcos -sinxsin
-sinxsin =
= (cosx-sinx)=-
(cosx-sinx)=-


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
| a |
| b |
| π |
| 2 |
| π |
| 2 |
| a |
| b |
| x |
| a |
| b |
| y |
| a |
| b |
| x |
| y |
| k+t2 |
| t |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com