
已知椭圆 的焦距为2,且过点
的焦距为2,且过点 .
.
(1)求椭圆C的方程;
(2)设椭圆C的左右焦点分别为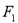 ,
,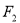 ,过点
,过点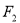 的直线
的直线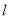 与椭圆C交于
与椭圆C交于 两点.
两点.
(1)当直线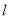 的倾斜角为
的倾斜角为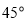 时,求
时,求 的长;
的长;
(2)求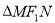 的内切圆的面积的最大值,并求出当
的内切圆的面积的最大值,并求出当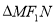 的内切圆的面积取最大值时直线
的内切圆的面积取最大值时直线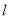 的方程.
的方程.
(1)椭圆C的方程为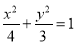 ;(2)(1)
;(2)(1)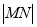 的长为
的长为 ;(2)当
;(2)当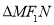 的内切圆的面积取最大值时直线
的内切圆的面积取最大值时直线 的方程为
的方程为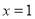 .
.
【解析】
试题分析:(1)由已知得 ,且
,且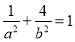 ,联立可求得椭圆方程;
,联立可求得椭圆方程;
(2)(1)联立椭圆与直线方程,由弦长公式可直接求出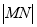 的长;(2)设直线
的长;(2)设直线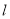 的方程为
的方程为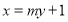 ,与椭圆方程联立消去
,与椭圆方程联立消去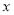 ,得
,得 ,而
,而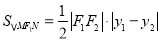 ;
;
利用均值不等式和函数单调性的性质可得当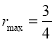 时,
时,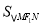 有最大值3,这时
有最大值3,这时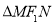 的内切圆面积的最大值为
的内切圆面积的最大值为 ,直线
,直线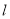 的方程为
的方程为 .
.
试题解析:(1)由已知,得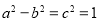 ,且
,且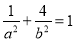 ,解得
,解得 ,
,
故椭圆C的方程为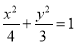 ; 4分
; 4分
(2)(1)由 ,消去
,消去 得
得 , 6分
, 6分
则 ; 9分
; 9分
(2)设直线 的方程为
的方程为 ,由
,由 ,得
,得 ,显然
,显然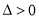 ,
,
设 ,则有
,则有 ,
,
设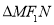 的内切圆半径为
的内切圆半径为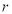 ,由
,由 可知,
可知,
当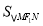 最大时,
最大时,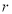 也最大,
也最大,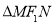 的内切圆面积也最大.
的内切圆面积也最大.
由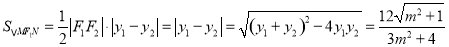 12分
12分
令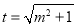 ,则
,则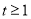 ,且
,且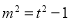 ,则
,则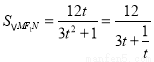 ,
,
令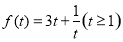 ,则
,则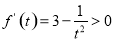 ,从而
,从而 在区间
在区间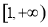 上单调递增,故有
上单调递增,故有
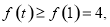 所以
所以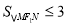 ,即当
,即当 ,
,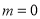 时,
时,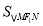 有最大值3,即
有最大值3,即 ,
,
这时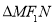 的内切圆面积的最大值为
的内切圆面积的最大值为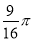 ,直线
,直线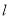 的方程为
的方程为 . 14分
. 14分
考点:椭圆的基本性质、直线与椭圆的位置关系、函数与方程思想.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第3课时练习卷(解析版) 题型:填空题
直线l经过点(3,0),且与直线l′:x+3y-2=0垂直,则l的方程是______________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第10课时练习卷(解析版) 题型:填空题
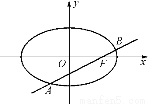
已知椭圆C: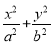 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为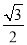 ,与过右焦点F且斜率为k(k>0)的直线相交于A、B两点.若
,与过右焦点F且斜率为k(k>0)的直线相交于A、B两点.若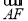 =3
=3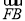 ,则k=________.
,则k=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西工大附中高三上学期第四次适应性训练理数学卷(解析版) 题型:选择题
执行右面的程序框图,若输入N=2013,则输出S等于( )

A.1 B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西工大附中高三上学期第四次适应性训练文数学卷(解析版) 题型:解答题
已知公比不为1的等比数列 的前
的前 项和为
项和为 ,
, ,且
,且 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西安铁一中国际合作学校高三下第一次模拟考试理科数学试卷(解析版) 题型:选择题
A.不等式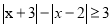 的解集为
的解集为
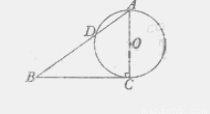
B.如图,已知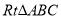 的两条直角边
的两条直角边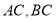 的长分别为3cm,4cm,以
的长分别为3cm,4cm,以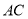 为直径的圆与
为直径的圆与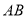 交于点
交于点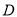 ,则
,则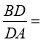 .
.
C.已知圆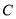 的参数方程为
的参数方程为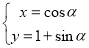 (
(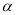 为参数)以原点为极点,
为参数)以原点为极点,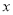 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线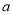 的极坐标方程为
的极坐标方程为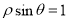 ,则直线
,则直线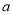 与圆
与圆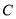 的交点的直角坐标系为_______
的交点的直角坐标系为_______
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省高考前30天数学保温训练8数列(解析版) 题型:选择题
将1,2,…,9这9个数平均分成三组,则每组的三个数都可以成等差数列的概率为( )
A.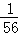 B.
B.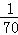 C.
C.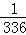 D.
D.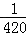
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com