
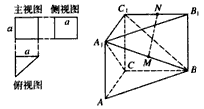
| 解:由三视图可知,在这个多面体的直观图中,AA1⊥平面ABC, 且AC⊥BC,AC=BC=CC1=a, (Ⅰ)连接AC1,AB1,因为BC⊥平面ACC1A1, 所以BC⊥AC1,在正方形ACC1A1中,A1C⊥AC1, 又因为BC∩A1C=C, 所以AC1⊥平面A1BC, 由正方形性质知AB1过A1B的中点M, 在△AB1C1中,MN∥AC1, 所以MN⊥平面A1BC。 |
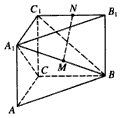 |
| (Ⅱ)由题意CA,CB,CC1两两垂直, 故以C为原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴, 建立空间直角坐标系, 又AC=BC=CC1=a,则B(0,a,0),B1(0,a,a),A(a,0,0), 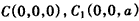 , ,则 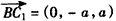 , ,又AC1⊥平面A1BC, 故 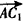 为平面A1BC的法向量, 为平面A1BC的法向量,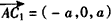 , ,所以, 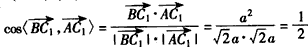 , ,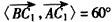 , ,因此直线BC1和平面A1BC所成角的大小为30°。 (Ⅲ)AB中点E的坐标为 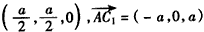 , ,易知 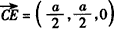 为平面AA1B的法向量,又 为平面AA1B的法向量,又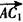 为平面A1BC的法向量, 为平面A1BC的法向量,设二面角A-A1B-C为θ, 则 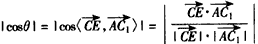 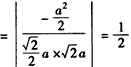 , ,由题意,知θ为锐角,所以θ=60°, 即二面角A-A1B-C为60°。 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
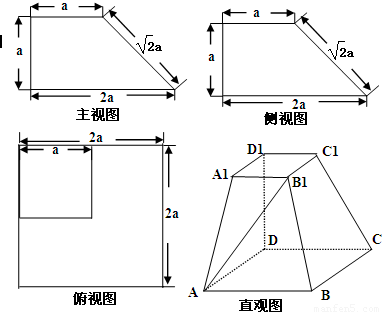
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年日照质检理)(12分)
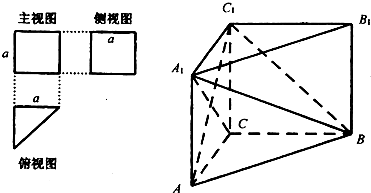
一个多面体的三视图及直观图如图所示,其中主视图和左视图都是边长为2的正方形,俯视图是腰长为2的等腰直角三角形,M、N分别是A1B、B1C1的中点。
(I)求证:MN⊥平面A1BC;
(II)求异面直线AM和CA1所成的角的大小;
(III)求二面角A―A1B―C的大小。
|
查看答案和解析>>
科目:高中数学 来源:2011年山东省淄博市高考数学二模试卷(理科)(解析版) 题型:解答题
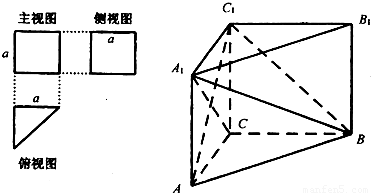
查看答案和解析>>
科目:高中数学 来源:2010年天津市河西区高考数学二模试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com