
【题目】已知函数![]() ,
, ![]()
(1)若![]() 在
在![]() 处取得极值,求
处取得极值,求![]() 的值;
的值;
(2)求![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(3)在(1)的条件下,若![]() ,求证:当
,求证:当![]() ,恒有
,恒有![]()
【答案】(1) ![]() (2) 当
(2) 当![]() 时,
时, ![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ;当
;当![]() 时,
时, ![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() (3)见解析
(3)见解析
【解析】试题分析:(1) ![]() ,又
,又![]() ,易得:
,易得: ![]() ,检验满足题意即可;
,检验满足题意即可;
(2)对![]() 分类讨论,明确函数的单调性,从而得到
分类讨论,明确函数的单调性,从而得到![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(3)欲证![]() ,只需证
,只需证![]() ,即证
,即证![]() ,即
,即![]() ,
,
设![]() ,求函数
,求函数![]() 的最小值大于零即可.
的最小值大于零即可.
试题解析:
(1)由![]() ,定义域为
,定义域为![]()
得![]()
因为函数![]() 在
在![]() 处取得极值,
处取得极值,
所以![]() ,即
,即![]() ,解得
,解得![]()
经检验,满足题意,所以![]() 。
。
(2)由(1)得![]()
![]() ,定义域为
,定义域为![]()
当![]() 时,由
时,由![]() 得
得![]() ,且
,且![]()
当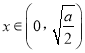 时,
时, ![]() ,
, ![]() 单调递减,当
单调递减,当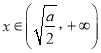 时,
时, ![]() ,
, ![]() 单调递增
单调递增
所以![]() 在区间
在区间![]() 上单调递增,最小值为
上单调递增,最小值为![]() ;
;
当![]() 时,
时, ![]()
当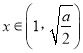 时,
时, ![]() ,
, ![]() 单调递减,当
单调递减,当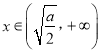 时,
时, ![]()
![]() ,
, ![]() 单调递增
单调递增
所以函数![]() 在
在![]() 处取得最小值
处取得最小值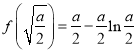
综上,当![]() 时,
时, ![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ;
;
当![]() 时,
时, ![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]()
(3)证明:由![]() 得
得![]()
当![]() 时,
时, ![]() ,
, ![]()
欲证![]() ,只需证
,只需证![]()
即证![]() ,即
,即![]()
设![]()
则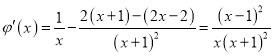
当![]() 时,
时, ![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递增。
上单调递增。
所以当![]() 时,
时, ![]() ,即
,即![]()
故![]()
所以当![]() 时,
时, ![]() 恒成立。
恒成立。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)数列{bn}的前n项和为Sn,求证:数列{Sn+![]() }是等比数列.
}是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=xlnx﹣ax2+(2a﹣1)x,a∈R.
(1)令g(x)=f′(x),求g(x)的单调区间;
(2)已知f(x)在x=1处取得极大值,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.
(1)证明:A=2B;
(2)若cosB= ![]() ,求cosC的值.
,求cosC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m、n是不同的直线,α、β是不重合的平面,则下列命题正确的是
A. 若α∥β,m![]() α,n
α,n![]() β,则m∥n
β,则m∥n
B. 若m![]() α,n
α,n![]() α,m∥β,n∥β,则α∥β
α,m∥β,n∥β,则α∥β
C. 若a![]() α,b
α,b![]() β,a∥b,则α∥β
β,a∥b,则α∥β
D. m、n是两异面直线,若m∥α,m∥β,且n∥α,n∥β,则α∥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2e2x+m|x|ex+1(m∈R)有四个零点,则m的取值范围为( )
A.(﹣∞,﹣e﹣ ![]() )
)
B.(﹣∞,e+ ![]() )
)
C.(﹣e﹣ ![]() ,﹣2)
,﹣2)
D.(﹣∞,﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列说法:①若![]() ,
,![]() ,则
,则![]() ;②若2
;②若2![]() =
=![]() ,
,![]() 分别表示
分别表示![]() 的面积,则
的面积,则![]() ;③两个非零向量
;③两个非零向量![]() ,若|
,若|![]() |=|
|=|![]() |+|
|+|![]() |,则
|,则![]() 与
与![]() 共线且反向;④若
共线且反向;④若![]() ,则存在唯一实数
,则存在唯一实数![]() 使得
使得![]() ,其中正确的说法个数为()
,其中正确的说法个数为()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com