
【题目】在三棱锥![]() 中,
中,![]() 和
和![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
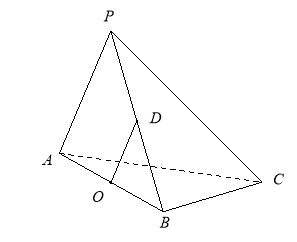
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)![]()
【解析】本题主要考查直线与平面平行的判定,以及平面与平面垂直的判定和三棱锥的体积的计算,体积的求解在最近两年高考中频繁出现,值得重视.
(1)欲证OD∥平面PAC,根据直线与平面平行的判定定理可知只需证OD与平面PAC内一直线平行,而OD∥PA,PA平面PAC,OD平面PAC,满足定理条件;
(2)欲证平面PAB⊥平面ABC,根据面面垂直的判定定理可知在平面PAB内一直线与平面ABC垂直,而根据题意可得PO⊥平面ABC;
(3)根据OP垂直平面ABC得到OP为三棱锥P-ABC的高,根据三棱锥的体积公式可求出三棱锥P-ABC的体积.
解:(Ⅰ)![]() 分别为
分别为![]() 的中点,
的中点,
![]()
![]() ∥
∥![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() ∥平面
∥平面![]() . ………………5分
. ………………5分
(Ⅱ)连结![]() ,
,![]()
![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,
![]() ⊥
⊥![]() ,
,![]() .
.
同理, ![]() ⊥
⊥![]() ,
,![]() .
.
又![]() ,
,![]() ,
,
![]() ,
,![]() ⊥
⊥![]() .
.
![]()
![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ,
,
![]() ⊥平面
⊥平面![]() .
.
又![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ⊥平面
⊥平面![]() .…………………10分
.…………………10分
(Ⅲ)由(Ⅱ)可知![]() 垂直平面
垂直平面![]()
![]()
![]() 为三棱锥
为三棱锥![]() 的高,且
的高,且![]()
![]() . …………………………14分
. …………………………14分


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知cosB=![]() ,a=5c.
,a=5c.
(1)求sinC的值;
(2)若△ABC的面积S=![]() sinAsinC,求b的值.
sinAsinC,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
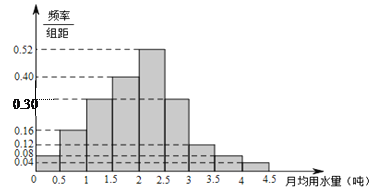
(1)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(2)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
(3)利用分层抽样的方法在[0,0.5) [3.5,4) [4,4.5)三组中选取5位居民,再从这5位居民中任意取三人,求这三人恰有两人来自同一组的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形, ![]() 平面
平面![]() ,
, ![]() ,且
,且![]() ,
, ![]() .
.
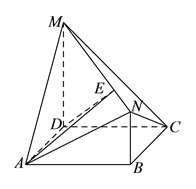
(I)求证: ![]() 平面
平面![]() .
.
(II)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(III)![]() 为直线
为直线![]() 上一点,且平面
上一点,且平面![]() 平面
平面![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①“若![]() 为
为![]() 的极值点,则
的极值点,则![]() ”的逆命题为真命题;
”的逆命题为真命题;
②“平面向量![]() 的夹角是钝角”的充分不必要条件是
的夹角是钝角”的充分不必要条件是![]()
③若命题![]() ,则
,则![]()
④函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
其中不正确的个数是
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在![]() 上的函数
上的函数![]() ,其图象是连续不断的,且存在常数
,其图象是连续不断的,且存在常数![]() 使得
使得![]() 对任意的实数
对任意的实数![]() 都成立,则称
都成立,则称![]() 是一个“
是一个“![]() 特征函数”则下列结论中正确的个数为( ).
特征函数”则下列结论中正确的个数为( ).
①![]() 是常数函数中唯一的“
是常数函数中唯一的“![]() 特征函数”;
特征函数”;
②![]() 不是“
不是“![]() 特征函数”;
特征函数”;
③“![]() 特征函数”至少有一个零点;
特征函数”至少有一个零点;
④![]() 是一个“
是一个“![]() 特征函数”;.
特征函数”;.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com