已知l1:2x+y+6=0与l2:3x-4y-6=0.
(1)求与l2相距为2的直线l的方程;
(2)求l1与l2的夹角的余弦值.
【答案】
分析:(1)设直线l:3x-4y+m=0,利用两条直线的距离公式建立关于m的方程,解出m=-16或4,可得所求直线l方程;
(2)利用两条直线的夹角公式,算出l
1与l
2的夹角θ满足tanθ=
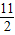
,再利用同角三角函数的关系即可算出l
1与l
2的夹角的余弦值.
解答:解:(1)设直线l:3x-4y+m=0.
∵直线l与l
2相距为2
∴
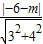
=2,解之得m=-16或4
因此直线l方程为3x-4y-16=0或3x-4y+4=0.
(2)求得l
1与l
2的斜率分别为k
1=-2,k
2=

设l
1与l
2的夹角为θ,则tanθ=
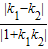
=
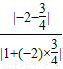
=
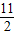
由此可得cosθ=
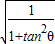
=
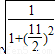
=
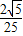
即l
1与l
2的夹角的余弦值等于
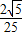
.
点评:本题给出两条直线,求它们夹角的余弦之值.着重考查了两条直线的距离公式、夹角公式和同角三角函数的基本关系等知识,属于中档题.

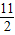 ,再利用同角三角函数的关系即可算出l1与l2的夹角的余弦值.
,再利用同角三角函数的关系即可算出l1与l2的夹角的余弦值.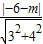 =2,解之得m=-16或4
=2,解之得m=-16或4
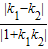 =
=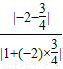 =
=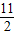
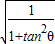 =
=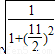 =
=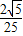
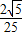 .
.

 备战中考寒假系列答案
备战中考寒假系列答案