
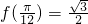 ;
; ,则角α的最小正值为
,则角α的最小正值为 ;
;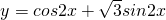 的图象向右平移
的图象向右平移 个单位得到.
个单位得到.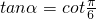 ,故角α的最小正值为
,故角α的最小正值为 ;
;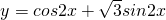 =2sin(2x+
=2sin(2x+ )=2sin[2(x+
)=2sin[2(x+ )],从而可得结论.
)],从而可得结论.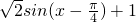 ,周期为2π,∴y=|f(x)|的周期为π,故①不正确;
,周期为2π,∴y=|f(x)|的周期为π,故①不正确;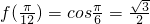 ,故②正确;
,故②正确;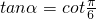 ,∴角α的最小正值为
,∴角α的最小正值为 ,故③正确;
,故③正确;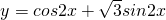 =2sin(2x+
=2sin(2x+ )=2sin[2(x+
)=2sin[2(x+ )],∴函数y=2sin2x的图象可由函数
)],∴函数y=2sin2x的图象可由函数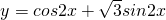 的图象向右平移
的图象向右平移 个单位得到,故④不正确
个单位得到,故④不正确

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:
 下列四个命题中,真命题的序号有
下列四个命题中,真命题的序号有| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 下列四个命题中,真命题的序号有
下列四个命题中,真命题的序号有| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
①将函数y=|x+1|的图象按向量v=(-1,0)平移,得到的图象对应的函数表达式为y=|x|
②圆x2+y2+4x+2y+1=0与直线y=![]() x相交,所得弦长为2
x相交,所得弦长为2
③若sin(α+β)=![]() ,sin(α-β)=
,sin(α-β)=![]() ,则tanαcotβ=5
,则tanαcotβ=5
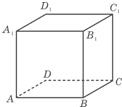
④如图,已知正方体ABCD-A1B

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com