练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本小题满分高☆考♂资♀源*网12分）

    设函数。

    （1）当a=1时，求的单调区间。

    （2）若在上的最大值为，求a的值。

    【解析】考查函数导数运算、利用导数处理函数最值等知识。

        解：对函数求导得：，定义域为（0，2）

    单调性的处理，通过导数的零点进行穿线判别符号完成。

    当a=1时，令

    当为增区间；当为减函数。

    区间上的最值问题，通过导数得到单调性，结合极值点和端点的比较得到，确定

    待定量a的值。

    当有最大值，则必不为减函数，且>0，为单调递增区间。

    最大值在右端点取到。。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （本小题满分14分高☆考♂资♀源*网）

    证明以下命题：

    对任一正整a,都存在整数b,c(b<c)，使得成等差数列。

    存在无穷多个互不相似的三角形△，其边长为正整数且成等差数列。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分高☆考♂资♀源*网12分）

    某迷宫有三个通道，进入迷宫的每个人都要经过一扇智能门。首次到达此门，系统会随机（即等可能）为你打开一个通道，若是1号通道，则需要1小时走出迷宫；若是2号、3号通道，则分别需要2小时、3小时返回智能门。再次到达智能门时，系统会随机打开一个你未到过的通道，直至走完迷宫为止。令表示走出迷宫所需的时间。

    求的分布列；

    求的数学期望。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分高☆考♂资♀源*网12分）

    设椭圆，抛物线。

    若经过的两个焦点，求的离心率；

    设A（0，b），,又M、N为与不在y轴上的两个交点，若△AMN的垂心为，且△QMN的重心在上，求椭圆和抛物线的方程。

    查看答案和解析>>

    科目：高中数学 来源：2010年郑州盛同学校高一下学期期末考试数学卷 题型：解答题

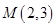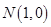    （本小题满分12分）光线自点射到点后被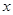轴反射，求该光线及反射光线所在的直线方程。（请用直线的一般方程表示解题结果）[来源:高&考

     

    查看答案和解析>>

    同步练习册答案