
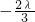 ,直线l1与l2相交于点P,其中λ∈R,
,直线l1与l2相交于点P,其中λ∈R,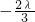 ,即-
,即- ,∴直线l2的方程为y-6=-
,∴直线l2的方程为y-6=-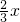 ,即2x+3y-18=0.
,即2x+3y-18=0. 解得
解得 .即点P(9,0).
.即点P(9,0). ,
,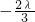 ,又
,又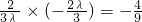 .
. ,于是
,于是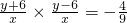 (x≠0),化为
(x≠0),化为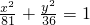 (x≠0).
(x≠0).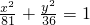 (去掉点(0,-6)).
(去掉点(0,-6)).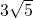 ,0),F(-
,0),F(-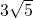 ,0),则满足|PE|+|PF|为定值.
,0),则满足|PE|+|PF|为定值. ,由课本椭圆一节的例题可知,点P的轨迹是一个椭圆,求出其方程,再求出其焦点,即选为点E、F,则可满足条件.
,由课本椭圆一节的例题可知,点P的轨迹是一个椭圆,求出其方程,再求出其焦点,即选为点E、F,则可满足条件.

科目:高中数学 来源: 题型:
| 2λ | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com