设a∈{1,2,3,4},b∈{2,4,8,12},则函数f(x)=x3+ax-b在区间[1,2]上有零点的概率为________.
分析:由f(x)在实数集上单调递增可知,要使函数f(x)=x
3+ax-b在区间[1,2]上有零点,只需满足条件
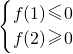
从而解得b-a≥1且b-2a≤8,后验证a,b即可获解.
解答:由f(x)在实数集上单调递增可知,要使函数f(x)=x
3+ax-b在区间[1,2]上有零点,只需满足条件
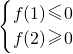
,
从而解得b-a≥1且b-2a≤8,∴a+1≤b≤2a+8,
∴当a=1时,b取2,4,8;
a=2时b取4,8,12;
a=3时,b取4,8,12;
a=4时b取8,12;
共11种取法,
又∵a,b的总共取法有16种,
故答案为:
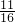
,
点评:本题是函数和概率的小综合题,其中关键有五点:(1)熟悉y=x
3及其系列函数的基本性质.(2)对函数零点概念理解,即图象与x轴恒有交点.(3)能正确的转化为条件组,(4)能正确的对a,b取值进行取舍.(5)熟悉等可能性事件概率计算.

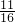
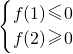 从而解得b-a≥1且b-2a≤8,后验证a,b即可获解.
从而解得b-a≥1且b-2a≤8,后验证a,b即可获解.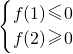 ,
,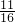 ,
,

 优百分课时互动系列答案
优百分课时互动系列答案