
【题目】正方体![]() 中,
中, ![]() 分别是
分别是![]() 的中点.
的中点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)在![]() 上求一点
上求一点![]() ,使得
,使得![]() 平面
平面![]() .
.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)以D为原点,DA,DC,D![]() 分别为x,y,z轴建立空间直角坐标系,
分别为x,y,z轴建立空间直角坐标系,
只需证明两平面的法向量数量积为0.(2)设![]() ,解得M(2,2λ,λ),由
,解得M(2,2λ,λ),由![]() 平面
平面![]() ,需
,需![]() ,可求解。
,可求解。
试题解析: 证明:(Ⅰ)建立如图所示的空间直角坐标系D-xyz,
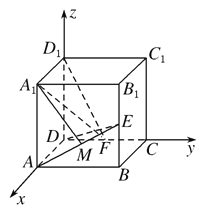
不妨设正方体的棱长为2,则A(2,0,0),E(2,2,1),F(0,1,0),A1(2,0,2), D1(0,0,2).
设平面AED的法向量为n1=(x1,y1,z1),则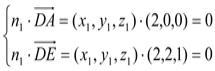
∴![]()
令y1=1,得n1=(0,1,-2).
同理可得平面A1FD1的法向量n2=(0,2,1).
∵n1·n2=0,
∴平面AED⊥平面A1FD1.
(Ⅱ)由于点M在AE上,
∴可设![]() =λ
=λ![]() =λ(0,2,1)=(0,2λ,λ),
=λ(0,2,1)=(0,2λ,λ),
可得M(2,2λ,λ),
于是![]() =(0,2λ,λ-2).
=(0,2λ,λ-2).
要使A1M⊥平面DAE,需A1M⊥AE,
∴![]() ·
·![]() =(0,2λ,λ-2)·(0,2,1)=5λ-2=0,得λ=
=(0,2λ,λ-2)·(0,2,1)=5λ-2=0,得λ=![]() .
.
故当AM=![]() AE时,即点M坐标为(2,
AE时,即点M坐标为(2,![]() ,
,![]() )时,A1M⊥平面DAE.
)时,A1M⊥平面DAE.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=x![]() (m∈N*).
(m∈N*).
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
(2)若该函数还经过点(2, ![]() ),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
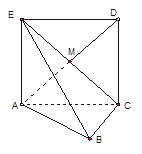
【题目】如图,边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M,![]() ,且AC=BC.
,且AC=BC.
(1)求证:![]() 平面EBC;
平面EBC;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线L的参数方程为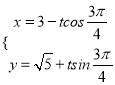 (
(![]() 为参数).在以原点
为参数).在以原点 ![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标中,圆C的方程为
轴正半轴为极轴的极坐标中,圆C的方程为![]() .
.
(Ⅰ)写出直线L的倾斜角![]() 和圆C的直角坐标方程;
和圆C的直角坐标方程;
(Ⅱ)若点 P坐标为![]() ,圆C与直线L交于 A,B两点,求|PA|
,圆C与直线L交于 A,B两点,求|PA|![]() |PB|的值.
|PB|的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l、m,平面α、β,下列命题正确的是 ( )
A. l∥β,lαα∥β
B. l∥β,m∥β,lα,mαα∥β
C. l∥m,lα,mβα∥β
D. l∥β,m∥β,lα,mα,l∩m=Mα∥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人玩掷骰子游戏,甲掷出的点数记为![]() ,乙掷出的点数记为
,乙掷出的点数记为![]() ,
,
若关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根时甲胜;方程有
有两个不相等的实数根时甲胜;方程有
两个相等的实数根时为“和”;方程没有实数根时乙胜.
(1)列出甲、乙两人“和”的各种情形;
(2)求甲胜的概率.
必要时可使用此表格

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为![]() ,答对文科题的概率均为
,答对文科题的概率均为![]() ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届广东省珠海市高三上学期期末考试文数】已知函数![]() 的最小值为0,其中
的最小值为0,其中![]() ,设
,设![]() .
.
(1)求![]() 的值;
的值;
(2)对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)讨论方程![]() 在
在![]() 上根的个数.
上根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 在平面直角坐标系
在平面直角坐标系![]() 下的参数方程为
下的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的普通方程及极坐标方程;
的普通方程及极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() :
: ![]() 与曲线
与曲线![]() 交于点
交于点![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com