
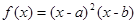 (
( ).
).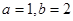 时,求曲线
时,求曲线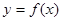 在点
在点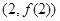 处的切线方程;
处的切线方程; 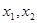 是
是 的两个极值点,
的两个极值点,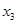 是
是 的一个零点
的一个零点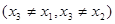 .证明:存在实数
.证明:存在实数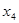 ,使得
,使得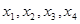 按某种顺序排列后构成等差数列,并求
按某种顺序排列后构成等差数列,并求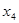 .
. .②存在实数
.②存在实数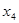 满足题意,且
满足题意,且 .
.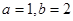 时,
时, ,故
,故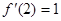 ,又
,又 ,
, 点
点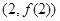 处的切线方程为:
处的切线方程为: .
.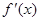 =
= ,由于
,由于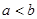 ,故
,故 ,
, 的两个极值点为
的两个极值点为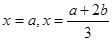 ,不妨设
,不妨设 ,
,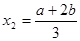 ,
, ,且
,且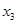 是
是 的一个零点,故
的一个零点,故 ,
,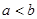 ,故
,故 ,故
,故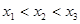 ,又
,又 ,
,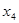 =
= ,此时
,此时 依次成等差数列,
依次成等差数列,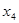 满足题意,且
满足题意,且 .
.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com