
【题目】设f(x)=lg(10x+1)+ax是偶函数,g(x)= ![]() 是奇函数,那么a+b的值为( )
是奇函数,那么a+b的值为( )
A.1
B.﹣1
C.﹣ ![]()
D.![]()
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图,一个正六角星薄片(其对称轴与水面垂直)匀速地升出水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(t)的图象大致为( ) 
A.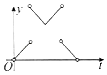
B.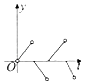
C.
D.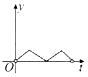
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a∈R,函数f(x)=cosx(asinx﹣cosx)+cos2( ![]() ﹣x)满足f(﹣
﹣x)满足f(﹣ ![]() )=f(0).
)=f(0).
(1)求f(x)的单调递减区间;
(2)设锐角△ABC的内角A,B,C所对的边分别为a,b,c,且 ![]() =
= ![]() ,求f(A)的取值范围.
,求f(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式组  所表示的平面区域为Dn , 记Dn内的整点个数为an(n∈N*).(整点即横坐标和纵坐标均为整数的点)
所表示的平面区域为Dn , 记Dn内的整点个数为an(n∈N*).(整点即横坐标和纵坐标均为整数的点)
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记数列{an}的前n项和为Sn , 且 ![]() ,若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
,若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为1的正项数列{an}满足an+12+an2< ![]() ,n∈N* , Sn为数列{an}的前n项和.
,n∈N* , Sn为数列{an}的前n项和.
(1)若a2= ![]() ,a3=x,a4=4,求x的取值范围;
,a3=x,a4=4,求x的取值范围;
(2)设数列{an}是公比为q的等比数列,若 ![]() <Sn+1<2Sn , n∈N* , 求q的取值范围;
<Sn+1<2Sn , n∈N* , 求q的取值范围;
(3)若a1 , a2 , …,ak(k≥3)成等差数列,且a1+a2+…+ak=120,求正整数k的最小值,以及k取最小值时相应数列a1 , a2 , …,ak .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn , 且an= ![]() (n∈N*). (Ⅰ)若数列{an+t}是等比数列,求t的值;
(n∈N*). (Ⅰ)若数列{an+t}是等比数列,求t的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)记bn= ![]() +
+ ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有4个编号依次为1、2、3、4的球,这4个球除号码外完全相同,先从盒子中随机取一个球,该球的编号为X,将球放回袋中,然后再从袋中随机取一个球,该球的编号为Y
(1)列出所有可能结果.
(2)求事件A=“取出球的号码之和小于4”的概率.
(3)求事件B=“编号X<Y”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com