练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，一个正六角星薄片（其对称轴与水面垂直）匀速地升出水面，直到全部露出水面为止，记时刻t薄片露出水面部分的图形面积为S（t）（S（0）=0），则导函数y=S'（t）的图象大致为（ ）
    A.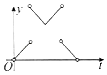
    B.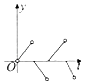
    C.
    D.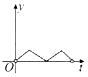

    【答案】A
    【解析】解：总面积一直保持增加，则导数值一直为正，故排除B； 总面积的增加速度是逐渐增大→突然变大→逐渐减小→逐渐增大→突然变小→逐渐变小，
    故导函数y=S'（t）的图象应是匀速递增→突然变大→匀速递减→匀速递增→突然变小→匀速递减，
    故排除CD，
    故选．A
    【考点精析】关于本题考查的利用导数研究函数的单调性，需要了解一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=Acos（ωx+φ）（其中A＞0，ω＞0，﹣ ＜φ＜ ）的图象如图所示，为得到的g（x）=Acosωx的图象，可以将f（x）的图象（ ）
    A.向左平移
    B.向左平移
    C.向右平移
    D.向右平移

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了测量山顶M的海拔高度，飞机沿水平方向在A，B两点进行测量，A，B，M在同一个铅垂面内（如图）．能够测量的数据有俯角、飞机的高度和A，B两点间的距离．请你设计一个方案，包括：
    （1）指出需要测量的数据（用字母表示，并在图中标出）；
    （2）用文字和公式写出计算山顶M海拔高度的步骤．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设向量 =（sinx， cosx）， =（﹣1，1）， =（1，1），其中x∈（0，π]．
    （1）若（ + ）∥ ，求实数x的值；
    （2）若 = ，求函数sinx的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，已知（a2+b2）sin（A﹣B）=（a2﹣b2）sin（A+B），则△ABC的形状（ ）
    A.等腰三角形
    B.直角三角形
    C.等腰直角三角形
    D.等腰三角形或直角三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： =1（a＞b＞0）的离心率为 ，且经过点（1， ），F1 ， F2是椭圆的左、右焦点．
    （1）求椭圆C的方程；
    （2）点P在椭圆上运动，求|PF1||PF2|的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知⊙M：（x+1）2+y2= 的圆心为M，⊙N：（x﹣1）2+y2= 的圆心为N，一动圆M内切，与圆N外切． （Ⅰ）求动圆圆心P的轨迹方程；
    （Ⅱ）设A，B分别为曲线P与x轴的左右两个交点，过点（1，0）的直线l与曲线P交于C，D两点．若 =12，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）同时满足①f（x）为偶函数；②对任意x，有f（ ﹣x）=f（ +x），则函数f（x）的解析式可以是（ ）
    A.f（x）=cos2x
    B.
    C.f（x）=cos6x
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设f（x）=lg（10x+1）+ax是偶函数，g（x）= 是奇函数，那么a+b的值为（ ）
    A.1
    B.﹣1
    C.﹣
    D.

    查看答案和解析>>

    同步练习册答案